本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
坐标下降法是一种沿着单个坐标轴方向寻找函数极小值的函数优化算法
本文讲解坐标下降法的思想和算法流程,并通过一个例子讲解坐标下降法的代码实现
通过本文可以快速了解什么是坐标下降法,以及如何使用坐标下降法解决函数优化问题
本节讲解什么是坐标下降法,以及坐标下降法的算法流程
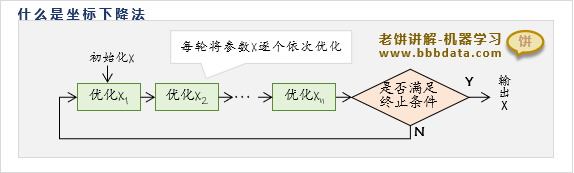
什么是坐标下降法
坐标下降法(Coordinate Descent)一种非梯度优化算法,它以逐坐标的方式来优化目标函数
简单来说,坐标下降法就是每次都将一个参数迭代到更优位置,如此反复使目标函数逐步下降
坐标下降法一般在目标函数可求单个变量的驻点时使用,即每次将单个参数迭代到它的驻点处
由于每次都将参数迭代到驻点,所以此时坐标下降法是极具优势的,往往很快就达到局部最优
✍️补充:为什么坐标下降法每次只迭代一个参数
坐标下降法每次只迭代一个参数,主要是考虑到单个参数的驻点相对较容易求得
如果可以同时求得多个参数的驻点,也可以每次把几个参数一起迭代,此时就称为"块坐标下降法"
坐标下降法算法流程
坐标下降法算法流程如下:
一、初始化
初始化参数X,可以采用随机初始化
二、逐坐标优化
1. 对所有随机(或按顺序)逐个优化:
(1) 计算当前的驻点
(2) 将x更新到驻点:
2. 检查是否满足终止条件
终止条件如下:
(1) 是否达到最大迭代次数
(2) 本次是否所有参数x的变化都很小
(3) 本次函数下降是否过小
三、输出
输出训练好的X
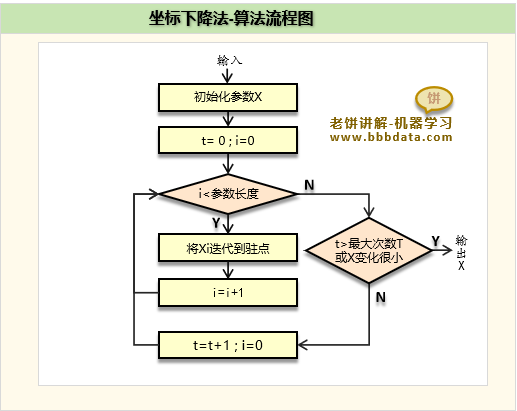
坐标下降法-算法流程图如下:
本节通过一个实例,讲解如何使用坐标下降法来解决函数优化问题
坐标下降法-代码例子
现求解 的极小值
计算的驻点,如下:
由 ,得到的驻点为:
由 ,得到的驻点为:
按照坐标下降法的算法流程,编写程序如下:
'''
坐标下降法代码示例
'''
import numpy as np
x = np.array([100,500]) # 初始化x
for i in range(100): # 迭代100次
old_x = x.copy() # 先保存好未更新的x
x[0] = x[1] # 更新x0到驻点
x[1] = x[0]/3 # 更新x1到驻点
y = -x[0]**2-3*x[1]**2+2*x[0]*x[1] # 计算目标函数值
print(f"第{i}轮迭代:x= {x},y={y}") # 打印结果
if (max(abs(old_x-x))<0.001): # 检查x是否变化都很小
break # 满足上述条件,则退出迭代运行结果如下:
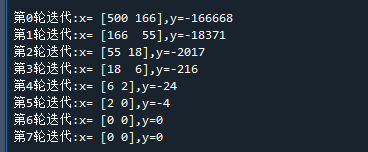
在第7轮迭代中,X没有变化,因此最终得到的解为x1=0,x2=0
可以看到,即使我们从一个很离谱的初始值,坐标下降法也能很快地迭代到局部最优解
End