本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
梯度下降算法是一种基本的函数优化算法,它利用函数的一阶信息来求解局部最小值
本文介绍梯度下降算法的原理,包括算法思想、算法流程、算法流程图等等
通过本文,可以了解梯度下降算法是什么,有什么用,以及梯度下降算法的算法流程
前言:为什么需要梯度下降算法
在单变量函数求取最小值问题中,通常只需要令的导数为0,然后解出就可以 了
然而,在多元函数中,求偏导令偏导为0,解出是非常困难的
虽然n个自变量,能求得n条偏导等式
然而,只有这n条等式是线性方程组时,我们才有系统的方法对其求解
而对于非线性方程组,我们目前并没有成熟的求解方案
Pass:这也是为什么我们很喜欢构造线性问题,因为它能轻松求解
由于联立偏导方程求精确解的路子行不通,
我们的替代方案就是进行数值求解,梯度下降法就是其中常用的方法之一
本节介绍梯度下降算法思想和原理,以及梯度的意义
梯度下降算法-思路概览
梯度下降法是常用于求函数最小值的一个基本算法,它的思路就是让目标函数不断往负梯度方向下降
梯度下降算法的思路如下:
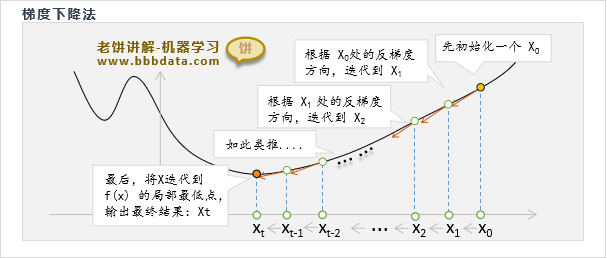
梯度下降算法先取一个初始值,然后进行迭代,每次都往梯度的反方向调整它
直到满足迭代条件(例如无法令目标函数值下降,或达到到最大迭代次数),则退出训练
负梯度与初始值的意义
梯度下降算法-负梯度的意义
在一元函数中,负梯度就是导数的反方向,在多元函数中,负梯度就是各个变量偏导数的反方向
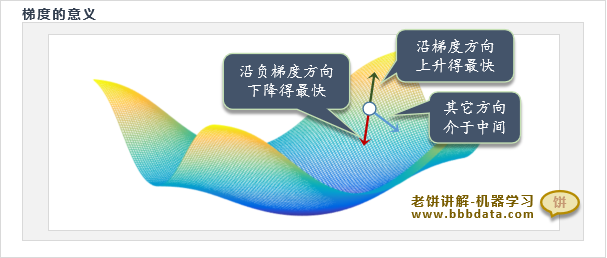
梯度是函数下降最快的方向(即调整相同步长,负梯度能令f(x)下降最快),故也称为最速下降法
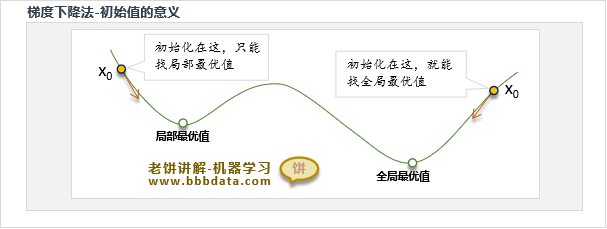
梯度下降算法-初始值的意义
从梯度下降算法原理,我们可以知道,梯度下降法对 x 的初始化非常敏感,
因为它只能找到离初始值最近的局部极小值,如果初始化不好,找到的结果也不好
最一般的初始化方法是随机初始化,然后多跑几次,看哪个结果好,就用哪一个
针对一些具体问题,也可能会设计一些专门用于该问题的初始化方法,这样效果会更好
梯度下降法的学习率
梯度下降算法设置学习率的目的是为了保证按负梯度方向调整一定能下降
由于负梯度方向能下降是瞬时的,如果调整步长过大,则不一定能保证函数能下降
由于需要保障调整步长足够小,使得目标函数能下降
因此,梯度下降法引入了学习率lr(learn rate)
即通过学习率控制调整的步长,以保障梯度下降算法能持续令目标函数下降
梯度下降算法的学习率一般设为0.1或0.01
本节讲解梯度下降算法的具体流程,以及展示算法流程图
梯度下降算法的流程与流程图
简单的说,梯度下降法就是先初始化 ,然后按 不断迭代就行
梯度下降算法的算法流程图如下:
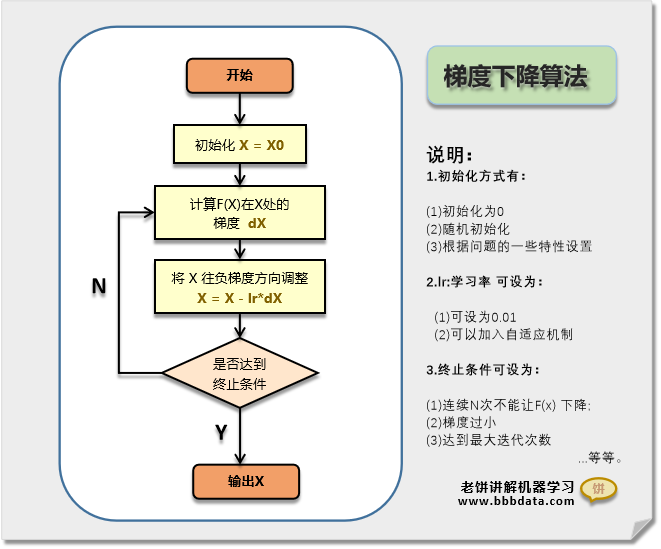
梯度下降算法流程与步骤如下:
1. 先初始化x的值 (按个人经验初始化,或随机初始化,或设为0)
2. 计算 在处的梯度,令,(lr为学习率,可设为0.1)
3. 计算在处的梯度,令
4. ...如此类推....一直到满足迭代终止条件,最后一次的即为所要找的解。
迭代终止条件:达到迭代次数,或者 与变化不大,或者与变化不大
在《梯度下降算法实例与代码》中,通过手算梯度下降算法过程,
可以更进一步了解梯度下降算法的具体过程与原理
以上就是梯度下降算法原理的所有内容了~
End