本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
逻辑回归是机器学习中必学的一个模型,它主要用于做二分类
本文基于前面的讲解,总结逻辑回归算法的原理、模型、损失函数、以及求解流程
通过本文,可以回顾逻辑回归算法的精要内容,巩固逻辑回归模型的学习与理解
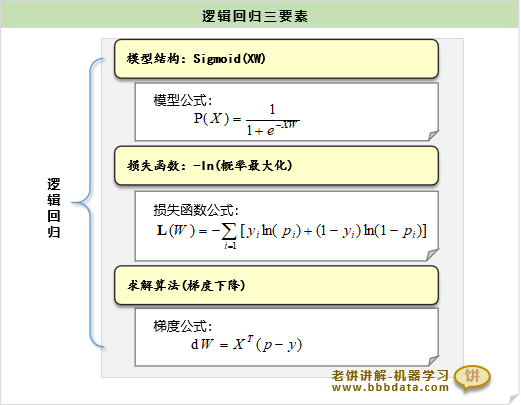
本节回顾和总结逻辑回归模型三组件:表达式、损失函数、求解算法
逻辑回归模型三组件回顾
逻辑回归模型是用于做二分类,它输出属于分类1的概率
模型的表达式、损失函数、求解算法如下:
模型表达式
逻辑回归的模型表达式如下:
从表达式可以看到,逻辑回归模型相当于用线性函数综合评估所有变量
再用sigmoid函数将综合评估值转换为概率值
损失函数
逻辑回归用概率最大化作为损失函数,即模型预测正确的概率最大
逻辑回归的交叉熵损失函数如下:
逻辑回归的模型求解
模型无法求得精确解,使用梯度下降等算法进行数值求解
逻辑回归损失函数的梯度公式为:
软件包里逻辑回归的求解用的不一定是梯度下降法,但思想是类似的
本节回顾梯度下降法求解逻辑回归的流程
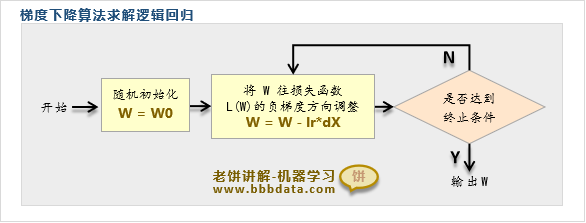
梯度下降法求解逻辑回归流程
梯度下降法求解逻辑回归的思路
梯度下降法求解逻辑回归的思路与流程如下:
1. 先求出待求解函数(损失函数)的梯度公式
2. 初始化一个初始解,根据梯度公式的负梯度方向,不断迭代
直到满足要求(例如达到最大迭代次数,或梯度过小)
👉说明
这里我们使用梯度下降法求解逻辑回归,主要是作为入门,可以顺带学习梯度下降算法,
而实际上,在软件包中,例如matlab,使用的就不是梯度下降法,而是牛顿法
在软件包的算法原理讲解时,我们可以看到,牛顿法会更为精妙和有效,它的求解速度更快
以上就是逻辑回归总结的全部内容了~
End