

本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
PCA主成份分析是一种常用的降维算法,一般使用SVD法来进行求解
本文讲解主成份分析PCA中主成份系数矩阵的求解原理,以及如何用代码具体实现
通过本文,可以了解PCA中的系数矩阵是怎么求解出来的,加深对PCA的理解
在讲解PCA中的主成份系数矩阵A的求解方法前,本节先PCA的数学表达
PCA的数学表述
PCA就是对样本进行旋转,使旋转后的样本每维之间互不相关

PCA的模型表示
由于旋转变换在数学中就是一个标准正交矩阵A
因此,PCA的模型表达式为:
其中,A为标准正交矩阵
✍️解释:它代表先将数据进行中心化,然后再进行旋转
PCA的求解目标
由于PCA要求旋转后的样本每个维度互不相关,即Y的协方差矩阵为对角矩阵
因此,PCA的求解目标函数为
其中, 为对角矩阵
PCA问题的简化
记,则有:
第2个等号中是需要证明的,即证明,这里省略
因此,PCA中的系数矩阵A的求解,可以化简为:
求一个标准正交矩阵A,使得:
这是一个经典的矩阵对角化问题
由于是对称矩阵,所以必存在一个标准正交矩阵A
本节讲解如何使用SVD法求解PCA主成份系数矩阵A
PCA主成份-SVD求解法
PCA的求解实际是矩阵对角化问题,理论上它可以通过特征值法来求解
但在实际中,更常用的是通过SVD分解来求得A
SVD分解是指将一个m*n的矩阵分解成三个矩阵的积,
其中U、V分别是m*m、n*n的酉矩阵,是对角矩阵
SVD法求解PCA的原理如下:
1. 注意到:
2. 只需将进行SVD分解,即有:
3. 由于SVD分解中的V是酉矩阵,易知:
当时,就是对角矩阵,如下
PCA主成份-求解流程(SVD法)
PCA的求解过程总结如下:
将进行SVD分解,得到
其中,1.就是所求
2.就是
本节讲解求解PCA的系数矩阵A的代码实现
求解PCA-调用sklearn
下面先通过sklearn包求解PCA中的系数矩阵A
具体代码实现如下:
"""
主成份分析求解DEMO(调用sklearn)
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
# 加载数据
iris = load_iris() # 加载iris数据
X = iris.data # 样本X
x_mean = X.mean(axis=0) # 样本的中心
# 用PCA对X进行主成份分析
clf = PCA() # 初始化PCA对象
clf.fit(X) # 对X进行主成份分析
# 打印结果
print('主成份系数矩阵A:\n A=',clf.components_) # 打印主成份系数
print('主成份方差var:',clf.explained_variance_) # 打印主成份方差var
print('主成份贡献占比(方差占比)Pr:',clf.explained_variance_ratio_) # 主成份贡献占比(方差占比)Pr:
# 获取主成份数据
y = clf.transform(X) # 通过调用transform方法获取主成份数据
y2 = (X-x_mean)@clf.components_.T # 通过调用公式计算主成份数据 运行结果如下:
求解PCA-自实现
下面不借助sklearn包,自行编写代码求解PCA的系数矩阵A
具体代码实现如下:
"""
主成份分析求解(自实现)
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
import numpy as np
from sklearn.datasets import load_iris
# 加载数据
iris = load_iris() # 加载iris数据
X = iris.data # 样本X
x_mean = X.mean(axis=0) # 样本的中心
# 通过SVD分解,得到A与XA每列的方差var
U,S,VT = np.linalg.svd((X-x_mean)/np.sqrt(X.shape[0]-1)) # 注意,numpy的SVD分解出的是US(VT)
A = VT.T # 主成份系数矩阵A
var = S*S # 方差
pr = var/var.sum() # 方差占比
#打印结果
print('主成份系数矩阵A:\n A=',A) # 打印主成份系数
print('主成份方差var:',var) # 打印主成份方差var
print('主成份贡献占比(方差占比)Pr:',pr) # 主成份贡献占比(方差占比)Pr:
# 获取主成份数据
y = (X-x_mean)@A # 通过调用公式计算主成份数据 运行结果如下: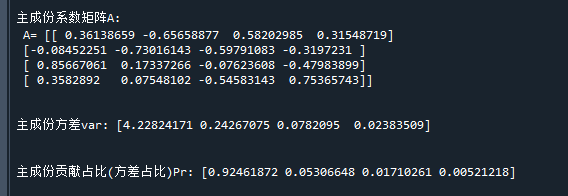
可以看到,自行编写代码的结果与调用sklearn包是一致的
没错,PCA的求解就是这么简单,仅是进行一下SVD分解即可
好了,以上就是PCA的求解方法以及代码实现了~
End