
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
相关系数是数据分析中一个常用的指标,它可用于检查变量间是否正负相关
本文介绍相关系数、相关系数矩阵的作用、原理,以及计算公式
通过本文,可以了解相关系数是什么,以及如何使用相关系数来评估变量的相关性
本节初步介绍相关系数的计算公式和相关系数的意义
相关系数计算公式
相关系数用于度量变量与变量之间的相关程度
相关系数的计算公式为:
从相关系数的公式易知道,相关系数取值范围在【-1,1】之间
相关系数主要用于检测变量之间的线性相关性,
相关系数r的意义如下:
👉1. 相关系数r越接近1,说明变量之间越正相关
👉2. 相关系数r越接近-1,说明变量之间越负相关
👉3. 相关系数r越接近0,说明变量之间不相关
总的来说,相关系数r的绝对值越大,相关性越强,|r|越小则相关性越弱
如何理解相关系数
相关系数的理解-标准化的协方差
相关系数公式也可以用以下形式表示
其中,
和实际是将原始标准化为标准差为1,均值为0的数据
从这个角度来看,相关系数其实就是将 和 进行标准化后,再对应相乘的总和,即求协方差
相关系数的理解-协方差的标准化
另一方面,相关系数也可以看作协方差的标准化(或单位化)
它将协方差的输出范围归一化到【-1,1】之间,如下:
本节讲解什么是相关系数矩阵,以及相关系数矩阵的计算方法
相关系数矩阵
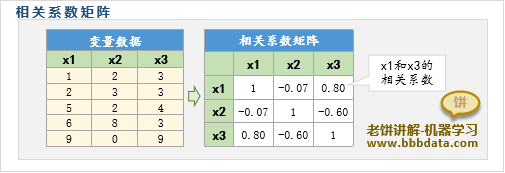
多个变量时,变量间两两之间的相关系数,就组成了相关系数矩阵
通过相关系数矩阵,可以比较一目了然看到变量间的相关性
通过下图可以清晰了解相关系数矩阵是个什么东东:
相关系数矩阵的计算公式 相关系数矩阵的计算公式如下:
1.先将X里每个变量进行标准化:
2.然后用标准化数据计算相关系数矩阵
说明:本公式不是数学上的严谨公式,更偏向于编程时的公式形式,仅供参考
"""
本代码用于展示相关系数矩阵的计算方法
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
import numpy as np
X = np.array([[1,2,3],[2,3,3],[5,2,4],[6,8,3],[9,0,9]]) # 原始数据
Xm = X.mean(axis = 0) # 原始数据各列的均值
std = np.sqrt(sum((X-Xm)*(X-Xm))) # 原始数据各列的标准差
Xn = (X - Xm)/std # 原始数据各列标准化
R = Xn.T@Xn # 相关系数矩阵
print('\n相关系数矩阵R:\n',R) # 打印相关系数矩阵运行结果如下:
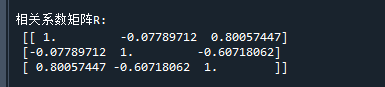
好了,相关系数的计算公式、意义和代码实现就介绍到这里了~
End