

本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
朴素贝叶斯模型是一个用于做分类的算法,它简单,易用,见效,是一个经典的算法
本文介绍朴素贝叶斯的相关概念、算法原理、计算公式,以及实际使用时的模型表示方法
通过本文,可以快速了解朴素贝叶斯模型是什么,以及朴素贝叶斯模型的参数估计方法
本节初步讲解朴素贝叶斯模型是个什么样的模型
什么是朴素贝叶斯模型
朴素贝叶斯模型思想
朴素贝叶斯是基于贝叶斯后验概率建立的模型,它用于解决分类问题,
朴素贝叶斯模型的思想如下:
它通过历史数据,利用贝叶斯原理对每个类别各自建立一个判别公式
模型预测时,分别用各个类别的判别公式进行预测,哪个判别值最大就判为哪个类别
什么是贝叶斯原理
贝叶斯原理为,在已知发生B条件下,发生A的概率为:
如果上述公式较抽象,可以将右边的分母移到左边,
则贝叶斯原理理解为:
即: 发生B,且发生A = 发生A,且发生B
本节介绍朴素贝叶斯模型中具体的公式及公式原理
朴素贝叶斯模型-原理讲解
朴素贝叶斯模型是基于贝叶斯原理构建出来的类别判别模型
朴素贝叶斯模型原理如下:
已知样本表现为X特征,想知道它属于类别 k 的概率,套用贝叶斯原理可得到:

进一步,假设各特征之间相互独立,那么特征的概率可以拆成累积形式,如下:

朴素贝叶斯中的"朴素",指的就是"各特征间互相独立"这一条件
由于最终比较的是各个类别概率的大小,而每个类别的概率公式的分母是一样的
因此,最终只需取上述概率公式中的分子部分作为判别公式来进行结果比较即可
最终即可得到朴素贝叶斯的判别公式如下:

其中,(1)式是贝叶斯判别器,(2)、(3)式是朴素贝叶斯概率公式和判别公式
公式(2)、(3)右边的概率一般由历史数据估算得到,从而得到左边的概率值或判别值
✍️关于朴素贝叶斯如何输出概率
有时我们希望模型输出每个类别的具体概率,理论上,只需按(2)中的概率公式就能得到各类别的概率
但实际中往往会发现各类别的概率之和不为一,这是因为实际中各个特征之间并不独立所造成的
因此,实际中如果需要输出概率,更一般的方法是直接将各类别的判别值进行归一化,作为概率值
朴素贝叶斯-模型与参数估算
朴素贝叶斯-判别公式
朴素贝叶斯模型的判别公式可记为如下:
其中, :样本X属于k类的判别值
:已知属于类别k时表现为的概率
:属于类别k的概率
朴素贝叶斯-参数估算
和一般用历史样本进行估计
的具体计算方法:
类别k中特征i为 的样本个数/ 类别k的样本个数
的具体计算方法:
类别k在总本样中的占比
备注:对于连续变量,在使用朴素贝叶斯模型时,需要先离散化成组别,这样才能统计占比
本节介绍在实际应用中,朴素贝叶斯模型中公式的计算方法
朴素贝叶斯-模型的表示
那么,在建模后,朴素贝叶斯模型长什么样呢?
由于朴素贝叶斯的对属于各类别的判别函数为:

那么,一个朴素贝叶斯判别模型可以由以下两个数据表示:
(1) 历史样本中,属于各类别的概率
(2) 历史样本中,特征表现概率表
也即最终建好的朴素贝叶斯模型就是两张表,如下:
1. 类别概率表:记录属于各个类别的概率
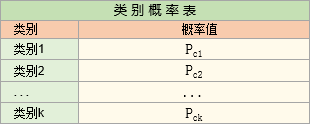
2. 一张特征概率表:记得各个特征,在类别k时表现为组别i的概率
备注:特征概率表实际是一组表,有多少个特征,就需要多少张特征概率表
在用历史数据估算出以上的类别概率表与特征概率表后,
当进来一个特征X时,按判别公式计算样本属于各个类别时的判别值即可
以上就是朴素贝叶斯模型原理的全部内容了~
End