

本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
矩阵的对角化,是指通过一个可逆P,将方阵A进行对角化,以简化矩阵对应的变换
本文讲解矩阵对角化的定义、本质与目的,并展示对角化的具体流程和代码实现
通过本文,可以了解什么是矩阵的对角化,对角化是为了什么,以及如何将矩阵对角化
本节讲解什么是矩阵的对角化,包括它的定义与本质
矩阵对角化的定义
矩阵的对角化是指:
对于矩阵A,求一个可逆P,使得是一个对角矩阵
数学表述如下:
其中,是一个对角矩阵
一般地,把 的各列称为A的特征向量
对角上的元素称为矩阵A的特征值
备注:矩阵的对角化只相对方阵而言,且,不是所有方阵都能对角化
如何理解矩阵对角化
矩阵与线性变换
不太严谨地说,变换就是把空间的一个向量,线性映射到该空间的另一个向量之中
线性变换可以使用矩阵来描述,对应地,每个矩阵,背后都指代着一个线性变换
如下所示,矩阵A所代表的变换,将向量(1,0)变换到了(1.5,0)中
因此每个矩阵A,都可以当作某个变换的数学描述
备注:矩阵A并不完全等价于变换,因为是绝对的,而A只是它的其中一种表述
如何理解矩阵的对角化
由可得:
即对于P的每一列都有:
即P的每一列在矩阵A指代的线性变换下,都保持方向不变,只是长度进行了的伸缩
所以矩阵的对角化,实际就是找出n个向量,这n个向量在A的变换下只进行伸缩
这n个在变换A下不变的向量,称为A的特征向量,它们的伸缩倍数则称为A的特征值
本节讲解矩阵对角化的基本目的,从而知道为什么要将矩阵对角化
矩阵对角化的基本目的
矩阵对角化的最基本目的是为了揭示矩阵A所对应的变换是个什么东西
由于A特征向量(即P)在变换A下只进行简单的伸缩
因此,如果把特征向量(即P)作为基,则可以简化变换
对于任意向量q,记它在基P下的坐标为,则:
由于每个在A所指代的线性变换下只进行简单的伸缩
因此有:
可得,的坐标为
因此,站在基P的角度来看,变换就是将变换为
即,站在基P的角度来看,
A所指代的变换表示为,它仅仅是将第i维进行的伸缩
因此,矩阵A对角化的意义就是,找出一个基P,使得在基P的视角下,变换A是一个对角变换
即矩阵对角化,可以换一个视角来简化变换A,从而更简单地、更本质地来研究、使用A
矩阵对角化的基本目的-举例
下面通过一个例子,展示矩阵对角化,是如何清晰的抓住矩阵对应的线性变换的特性的
设
将A进行对角化,可得:
未对角化前对线性变换的认识
以向量q = [1,0]为例,如果直接看A,
那么只知道它所指代的变换,会将q变换到,如下

光是这样看,是很难了解A所指代的变换的特性的,只知道它把(1,0)变换到了(1.5,0.5)
对角化后对线性变换的认识
通过对角化后,可得到,以P为基,则有:
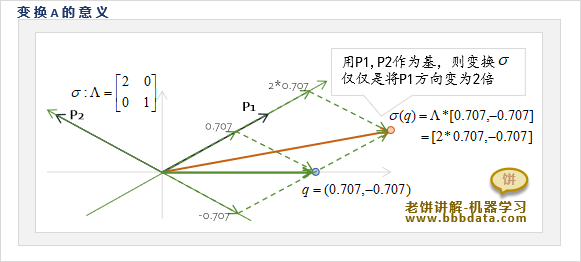
以P为基,变换其实就是将q点的P1、P2方向伸缩2、1倍
因此,变换在原来坐标系的表示为A,很难理解是个什么样的变换
而用P作为基,则就只是在各个坐标轴中进行伸缩的变换,一下子就简单得多了~
一个矩阵如果可以对角化,则说明它背后所指的变换实质是某组基下的伸缩变换
而变换总是各种各样的,并不永远都是伸缩变换,所以不会所有的矩阵都能对角化
本节展示如何对矩阵进行对角化,以及代码实现方法
矩阵对角化的理论方法
矩阵对角化的思路
由于对于每个特征向量有:
因此有:
即:
上式说明线性相关,因此:
而展开后是一个关于的n次多项式,即
求解多项式求得多个
将各个特征值代入,就可以解得对应的特征向量
矩阵对角化-例子解说
以 为例,将它对角化的实操过程如下:
1. 计算特征多项式
2. 求解特征值
由解得:
3. 求解特征向量
(1) 将代入 ,可得:
解得特征向量
(2) 将代入 ,可得:
解得特征向量
4. 组装与单位化P
将两个特征向量按列组装,可得到
进一步将它按列单位化后得到:
5. 验证
可进一步验证:
矩阵对角化-代码实现
在python中可以使用numpy来实现矩阵的对角化
具体代码示例如下:
import numpy as np
A = np.array([[1.5,0.5],[0.5,1.5]]) # 准备进行对角化的矩阵A
d,P = np.linalg.eig(A) # 计算特征值和特征向量
L = np.linalg.inv(P) @ A @ P # 对角化A
print("\n原始矩阵A:\n",A) # 打印原始矩阵A
print("\n特征向量矩阵P:\n",P) # 打印特征向量矩阵P
print("\n对角化后的特征值L:\n",L) # 打印对角化后的特征值L代码运行结果如下:
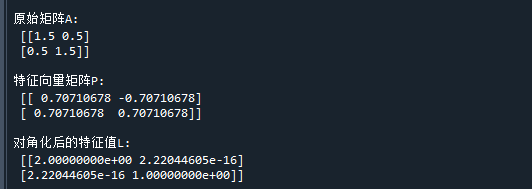
可以看到,使用矩阵P对A进行对角化后,得到了对角矩阵L
好了,以上就是矩阵的对角化,以及它的意义和对角化流程了~