本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
过拟合是机器学习中最常遇到的问题,它会导致模型在实际使用时的泛化能力差
本文讲解过拟合的两个例子,以及展示一个例子来说明过拟合产生的过程
通过本文,可以了解什么是过拟合,以及过拟合的危害,和为什么会产生过拟合
本节介绍什么是过拟合,以及过拟合的例子
什么是过拟合
过拟合是指在由于过度拟合训练数据,
导致模型过于复杂,以致于在测试数据上预测效果不好泛化能力差
过拟合例子
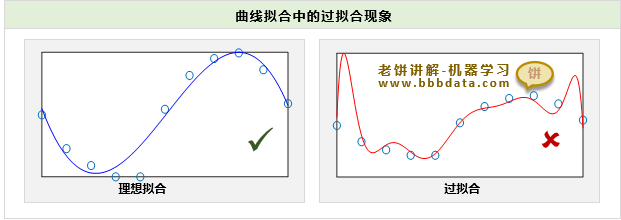
在曲线拟合中,过拟合的示例如下:
可以看到,在训练数据上,图1并没有图2拟合得好,但它更倾向数据的真实关系
图2为了尽量拟合每个训练样本点,导致曲线扭扭曲曲,偏离了原本应有的形态,我们称为过拟合
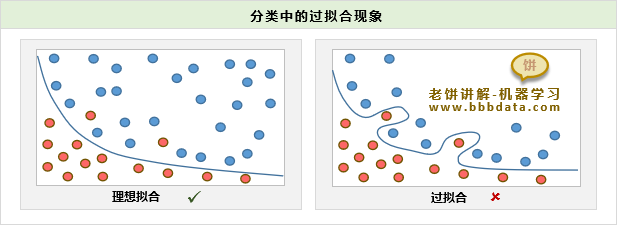
在曲线拟合中,过拟合的示例如下:
可以看到,过拟合时,模型虽然在训练数据上达到更好的效果,
但这种"更好的效果"是通过"勉强而为之"换取而来的,它对模型真实应用时有害无益
本节展示一个曲线拟合中出现过拟合的实验例子,更深刻理解过拟合
过拟合-实验例子
现有数据点如下:
我们用三次多项式 对数据点拟合如下:

蓝色为数据点,红色为多项式曲线
如果觉得还有些误差,不尽人意,
还可以强行用10次多项式 把每个点都拟合到位(拉格朗日插值法)
如下:
可以看到,10次多项式对训练数据已经是0误差拟合
虽然10次多项式对训练数据的拟合误差为0,但它却未必是我们想要的曲线
我们不妨把该10次多项式的曲线画出,如下:
可以看到整条拟合曲线非常的跌宕!
虽然它精确经过了每一个数据点,但在非历史数据点上,预测效果反而不如3次多项式~!
这就是过拟合,为了勉强拟合训练样本,而导致缺失泛化能力
实验总结
从这例子,我们看到了两个问题
1.强行拟合历史数据导致整体震荡
由于强行拟合,导致函数在数据点之间剧烈震荡,失去了预测的效果
2.强行拟合历史数据会复现不合理的错误
观察原始数据点,应该是一个三角函数sin的数据,
而在 x = -0.6 处,虽然数据点的 y 值是 -1.2,
但这实际上这更可能是一个采集错误的数据点
而10次多项式过于追求拟合,反而把这个错误数据点的错误也完美无遗的重现了出来
反观3次多项式,它兼顾了整体的平滑,成功忽略了这个错误点
好了,机器学习中的过拟合就介绍到这里了
End