本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
最小二乘法是线性回归的求解方法,它可以使最小二乘误差最小
本文介绍最小二乘法的原理,包括最小二乘法的求解公式与详细推导过程
通过本文,可以了解最小二乘法是如何求解线性回归的,以及它的公式推导
本节描述最小二乘问题的背景问题和它的求解公式
最小二乘法-原始问题
最小二乘问题
已采集 x 和 y 的m个样本
用矩阵表示的个样本,用维列向量 表示的个样本
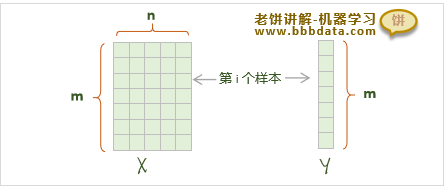
即X和Y的每一行代表一个样本
假设用来拟合 y ,则所有样本的预测误差平方和为:
现在我们要求解使E最小的w
最小二乘问题-数学表述
上述问题整理成一个更纯粹的数学问题,则为:
现有X,Y,求一w,
使 最小
该问题称为最小二乘问题
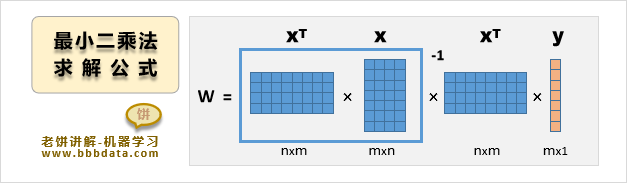
最小二乘问题的求解公式
上述最小二乘法问题的求解公式为:
如下图所示:
本节描述最小二乘法问题数学通用表述,这个表述更为常见通用
最小二乘法通用表述
上面的X,Y是我们采集到的数据,w是我们要求的解
事实上,更多时候我们喜欢用以下形式来描述该问题
问题表述
已知A,b,
其中A为矩阵,b为的列向量
求一 使与的误差平方和最小:
备注:该问题也可以理解为,求一使 最佳迫近
求解公式
对应的求解公式如下
本节讲述微分法推导最小二乘法的求解公式的过程
最小二乘法求解公式-推导思路
这里我们使用最小二乘法问题的通用表述进行推导求解公式
即求一令最小
推导思路很简单,
假设 ,
要使 最小,
只要令 分别对 的偏导为 0,
即有
求解上面的方程组即可求得令 最小的解
最小二乘法求解公式-推导过程
最小二乘法求解公式的详细推导过程如下:
最小二乘法的误差函数为:
先求单个x分量在E中的偏导,如下:
则对x的总偏导为:
令偏导为0,则可求得:
即有上述最小二乘法求解公式:
关于最小二乘法求解公式的另一种推导方法
最小二乘法求解公式还可以利用高等代数的方法进行推导
利用高等代数的方法进行推导最小二乘法的求解公式会更加简洁、直接、直观,
但由于依赖高等代数等相关知识,本文不再介绍,如有兴趣,可查看文章《最小二乘法》
以上就是最小二乘法的求解公式及公式的推导过程了~
End