本站原创文章，转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
最小二乘法可在线性方程组没有精确解时,求得最小二乘误差解
本文讲解什么是最小二乘问题、最小二乘问题如何求解以及求解公式的推导过程
通过本文可以快速了解最小二乘法是什么，解决什么问题，以及最小二乘法的推导原理
本节讲解最小二乘法是什么，以及最小二乘法求解公式
什么是最小二乘法
什么是最小二乘问题
现有 的矩阵，与列向量，求一个，使得
在上述问题可解的时候，只需左右两边取A的逆就可得到：
而当上述问题不可解时，即不存在这样一个 使得 的时候
则选择退而求其次，希望求一个 ，使得 的平方误差和最小
最小二乘问题就是指上述问题， 即求一x使得 Ax 最佳逼近 b
最小二乘法-求解公式
最小二乘问题在机器学习上是一个常见的问题，它可由最小二乘公式求得
最小二乘问题的求解公式为：
使用最小二乘公式求解最小二乘问题，则称为最小二乘法，是一个基本方法
本节讲解两种最小二乘法公式的推导方法以及推导过程
通过驻点推导-最小二乘法
最小二乘法的求解公式可以通过求误差函数的驻点来得到
即对总误差函数求偏导，令偏导为0，再联立解出x，推导过程如下：
一、最小二乘的误差函数
最小二乘的误差函数为：
二、求误差函数对x的偏导
先求x的单个分量的偏导，如下：
则对x的总偏导为：
三、求x的驻点
令误差函数的偏导为0，则可求得：
即可得到最小二乘法的求解公式：
通过最佳逼近-推导最小二乘法
通过代数中的空间最佳逼近原理也可推导最小二乘法，具体如下：
由于是对的最佳逼近，可知向量与构成的空间垂直
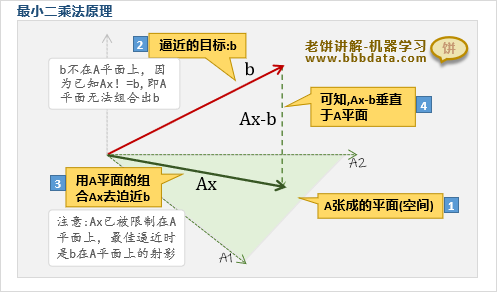
如图所示，Ax-b与A构成的空间垂直(即与A的每列的点积为0)，即有：
进一步化简即可得到：
通过驻点求导来推导最小二乘法，虽然推导过程较为复杂，但思路简洁，知识要求起点低
而最佳逼近方法，在了解代数基础上，推导最小二乘法基本就是一步到位，随时手推，不必记公式
End
