本站原创文章，转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
梯度下降法也称为最速下降法，是机器学习中一种基础的函数优化算法
本文讲解梯度下降算法的原理与算法流程，并展示梯度下降算法的一个具体例子
通过本文可以快速了解什么是梯度下降算法，以及如何使用梯度下降算法解决函数优化问题
本节介绍梯度下降算法的思想，快速了解梯度下降算法是什么
什么是梯度下降算法
梯度下降法是常用于函数优化的一个基本算法，它的思路是让目标函数不断往梯度方向下降
梯度下降算法的思路如下：
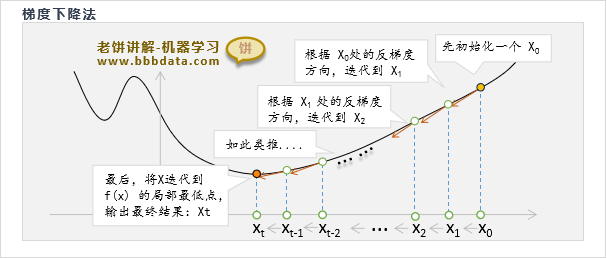
梯度下降算法先取一个初始值，然后进行迭代，每次都往梯度的反方向调整它
直到满足迭代条件（例如无法令目标函数值下降，或达到到最大迭代次数），则退出训练
负梯度与初始值的意义
梯度下降算法-负梯度的意义
在一元函数中，负梯度就是导数的反方向，在多元函数中，负梯度就是各个变量偏导数的反方向
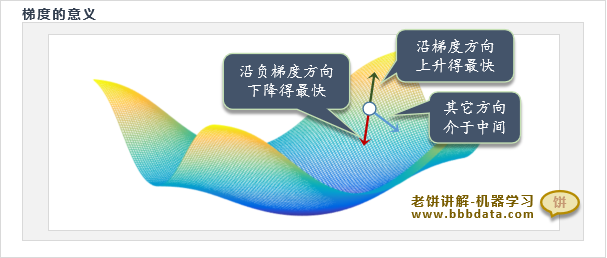
梯度是函数下降最快的方向(即调整相同步长，负梯度能令f(x)下降最快)，故也称为最速下降法
梯度下降算法-初始值的意义
从梯度下降算法原理，我们可以知道，梯度下降法对 x 的初始化非常敏感，
因为它只能找到离初始值最近的局部极小值，如果初始化不好，找到的结果也不好
往往是先随机初始化，然后多跑几次，看哪个结果好，就用哪一个
本节讲解梯度下降算法的具体流程，以及展示算法流程图
梯度下降算法的流程与流程图
简单的说，梯度下降法就是先初始化 ，然后按 不断迭代就行
梯度下降算法的算法流程图如下：
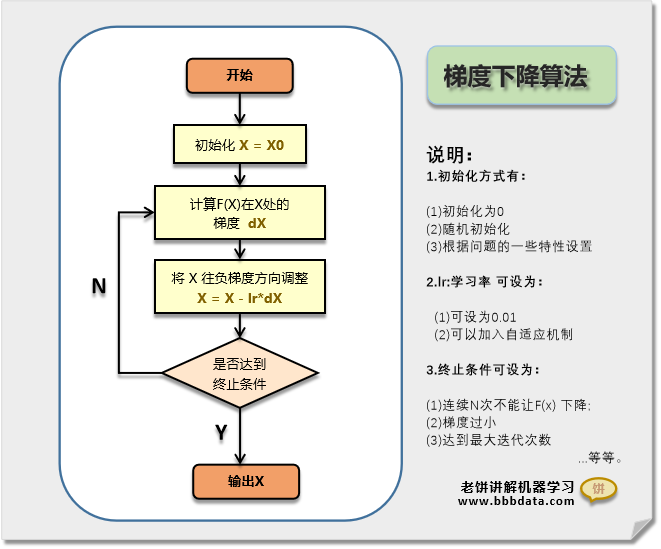
梯度下降算法流程与步骤如下：
1. 先初始化x的值 (按个人经验初始化，或随机初始化，或设为0)
2. 计算 在处的梯度,令,(lr为学习率，可设为0.1)
3. 计算在处的梯度,令
4. ...如此类推....一直到满足迭代终止条件，最后一次的即为所要找的解。
迭代终止条件：达到迭代次数，或者 与变化不大，或者与变化不大
在《梯度下降算法实例与代码》中，通过手算梯度下降算法过程，
可以更进一步了解梯度下降算法的具体过程与原理
本节利用python进行代码编程，展现如何用代码实现梯度下降算法
梯度下降算法的代码实现( python)
下面使用梯度下降算法来求函数的最小值
由于梯度下降法需要使用目标函数的梯度，所以需要先算出梯度，如下：
，
接下来只需按梯度下降算法的流程，让解不断地往负梯度方向迭代就可以了
梯度下降法具体实现代码如下：
# -*- coding: utf-8 -*-
"""
梯度下降求y= (x1-2)^2+(x2-3)^2的最小解
"""
import numpy as np
x = np.array([0,0]) # 初始化x
lr = 0.1 # 设置学习率
for i in range(100): # 最大迭代100次
dx = np.array([2*x[0]-4, 2*x[1]-6]) # 计算x的梯度
x = x - lr*dx # 往负梯度方向更新x
if((min(abs(dx))< 0.001) ):break # 如果梯度过小，则退出迭代
print("第"+str(i+1)+"轮迭代:x=:["+str(x[0])+","+str(x[1])+"],y="+str((x[0]-2)**2+(x[1]-3)**2))运行结果如下：
可以看到，经过38轮迭代，求得的 x1,x2= 【1.999,2.999】与真实极值【2,3】已经非常接近了
End