
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
层次聚类算法是一个基本的聚类算法,它一般以ward方差作为类别距离
本文讲解层次聚类算法以及ward方差的思想、计算公式,并展示如何自实现一个层次聚类算法
通过本文可以了解什么是层次聚类算法、什么是ward方差,以及如何自实现ward方差层次聚类算法
本节讲解什么是层次聚类算法以及ward方差
层次聚类算法与ward方差
什么是层次聚类算法
层次聚类算法(Hierarchical)是一种最基本的聚类算法,用于对样本进行聚类
它先将每个样本作为一类,然后逐步合并,是一种自下而上的聚类算法,如下:
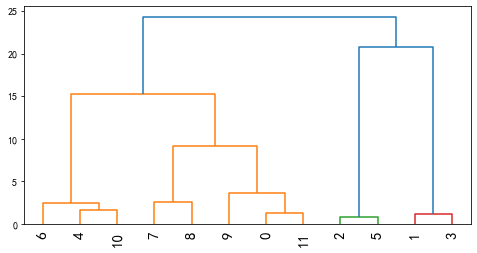
如图所示,从下往上,12个样本先各自作为一个类别,然后逐步合并为一个类别
层次聚类算法流程
层次聚类算法的流程如下:
1. 将每个样本初始化为一类,有多少个样本就有多少个类别
2. 计算类别两两之间的距离
3. 将距离最近的两个类别合并为一类
4. 计算新类别与其它类别的距离
重复3,4,直到只剩1个类别
而当层次聚类算法使用ward方差作为距离时,则称为层次聚类ward算法
Ward方差是什么
Ward方差法以类别u、v合并时,类内方差SSE的增加量作为u、v的距离d
即ward方差法的距离定义为:
其中,类别K的类内方差SSE定义为:
其中, :x的维度
:类别K的样本个数
:类别K的样本集合
即类别K的样本到类别K中心的方差总和
本节讲解以ward方差进行层次聚类时的算法流程以及相关计算公式
ward方差法的距离计算公式
ward方差法的初始距离
初始状态,每个样本独自作为一个类别,因此,此时所有类别的SSE都为0
则类别u与类别v之间的距离为:
作为简化,可以取为,即欧几里得距离的平方
ward方差法的距离更新
每次选择两个最小距离的类别进行合并后,需要计算新类别与其余类别的距离
如果每次都按上述定义公式计算,计算量会较大,所以一般使用如下迭代公式:
其中,u由s、t两个类别合并而成
代表的样本个数
备注:笔者也未验证上述迭代公式的推导过程,有兴趣的可按定义进行推导一下
层次聚类(ward连接)算法流程
层次聚类算法使用ward连接时,算法流程如下:
一、 初始化
(1) 每个样本作为一个类别
(2)计算每个类别的距离d
,dist是欧几里得距离
二、循环合并类别
循环合并类别,直到只剩一个类别:
(1) 将距离最近的两个类别s、t合并,得到新类别u
(2) 计算u与其它类别的距离
对于类别v,新类别u(由s,t合并而成)与v的距离为:
其中,代表的样本个数,
(3)记录本次合并的两个类别,以及它们的距离到"合并过程表"Z
三、输出
输出合并过程表Z
本节不借用软件包,展示如何自行实现层次聚类算法(ward方差法)
层次聚类ward算法-代码自实现
下面不借用软件包,自行实现层次聚类ward算法
具体代码如下:
备注:本代码主要扒自matlab的linkage函数,运行结果与matlab、scipy一致
x = [1 2 ; 3 4; 5 6 ;1 8;2 2]; % x
Y = pdist(x); % 计算距离,存放(1,2)(1,3),..,(1,n),(2,3),(2,4)..,(n-1,n)的距离
[k, n] = size(Y); % 距离向量的行与列
m = (1+sqrt(1+8*n))/2; % 当前类别个数
Z = zeros(m-1,3); % 初始化输出矩阵
N = zeros(1,2*m-1); % 类别样本个数
N(1:m) = 1; % 当前每个类别都是一个样本
n = m; % 总类别个数
R = 1:n; % 当前类别的编号
Y = Y .* Y; % 对距离Y平方
for s = 1:(n-1)
X = Y; % 将Y赋给X
[v, k] = min(X); % 找出最小距离
i = floor(m+1/2-sqrt(m^2-m+1/4-2*(k-1))); % 找出最小距离对应的i是当前第几个类别
j = k - (i-1)*(m-i/2)+i; % 找出最小距离对应的j是当前第几个类别
Z(s,:) = [R(i) R(j) v]; % 记录本次合并类别,R中存放的是类别编号
I1 = 1:(i-1); I2 = (i+1):(j-1); I3 = (j+1):m; % 临时变量
U = [I1 I2 I3]; % 剩余类别
I = [I1.*(m-(I1+1)/2)-m+i i*(m-(i+1)/2)-m+I2 i*(m-(i+1)/2)-m+I3]; % 剩余类别与i的距离索引(不包括j)
J = [I1.*(m-(I1+1)/2)-m+j I2.*(m-(I2+1)/2)-m+j j*(m-(j+1)/2)-m+I3]; % 剩余类别与j的距离索引 (不包括i)
Y(I) = ((N(R(U))+N(R(i))).*Y(I) + (N(R(U))+N(R(j))).*Y(J) - ...
N(R(U))*v)./(N(R(i))+N(R(j))+N(R(U))); % 更新距离
% ((剩余类别样本数+i的样本数)*剩余类别与i的距离
% +(剩余类别样本数+j的样本数)*剩余类别与j的距离
% -(剩余类别样本数)*ij距离)/(剩余类别样本数+i类别样本数+j类别样本数)
J = [J i*(m-(i+1)/2)-m+j]; % 与j连接的类别的距离索引 (包括i)
Y(J) = []; % 删除与j连接的类别的距离
m = m-1; % 更新类别个数
N(n+s) = N(R(i)) + N(R(j)); % 更新类别编号的样本个数
R(i) = n+s; % 将原存放i类别编号的位置改为新类别的编号
R(j:(n-1))=R((j+1):n); % 移动编号,覆盖掉j
end
Z(:,3) = sqrt(Z(:,3)) % 修改回欧几里得距离,就是最终聚类过程结果 运行结果如下:

Z记录了合并过程,三列各代表:类别1,类别2,距离
以第一行为例,即类别1与类别5的距离最小,距离为1,本次进行合并
End
 评论
评论