
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
因子分析FA是机器学习中常用的降维算法之一,它可以从数据中分解出隐因子
本文讲解因子分析的模型、思想以及损失函数等,并展示因子分析的具体使用例子
通过本文可以快速了解因子分析是什么,有什么用,以及如何使用因子分析进行降维
本节快速了解因子分析是什么,用来干什么
因子分析是干什么的
因子分析FA(Factor Analysis)是机器学习中一种常用的因子提取、变量降维技术
它假设我们所观察到的数据是由隐变量与噪声混合生成的,如下:
用数学表示,则x与h的关系为:
其中,
即背后存在一些隐变量h,且这些隐变量h之间都是两两独立标准正态分布的
而我们所观察到的x则是由这些隐变量h与常量u、噪声e混合之后衍生出来的
而因子分析则希望根据追溯出隐变量的值,即还原出背后后原始的、纯粹的本质因子
因子分析的用途
因子分析与声源分解
声源分解就是因子分析应用的一个经典场景
如下图所示,台上站着两个正在说话的人,并在台下三个不同方位放了3台录音机
台上的声音就是原始隐变量,而台下录制的声音就是我们事后能观察到的数据
由于距离不同,录音机以不同的权重接收声源,并受环境中的噪声e影响
而声源分解则是希望通过3个录音机录的数据,分解出两人的声音
因子分析与降维
因子分析在机器学习中也常常被用于降维,如下:
由于隐变量h是独立正态分布的,所以h的每个变量之间包含的信息更为"纯粹"
因此将x转换回h之后,所需要的变量往往更少,因此因子分析可以被用于降维
需要注意,通过因子分析进行的降维是有损降维,因为
因此,使用来将隐因子转换回原始数据时,实际是忽略了噪声的
本节讲解因子分析FA的模型表达式、损失函数以及求解主流程
因子分析-模型表达式
因子分析模型表达式-x与h的关系
因子分析假设由隐因子线性组合而成,并与常量、噪声叠加,如下:
其中, :观察到的数据
:生成x的隐变量
:隐变量h的权重
:h生成x时叠加的常量
:h生成x时叠加的噪声变量
且有:
,为对角矩阵
解释:每个隐因子都是一个独立的正态分布随机变量,每个隐因子的方差都为1
而每个x所受到的噪声也是独立的正态分布随机变量,但方差不一定相同
因子分析模型表达式-h与x的关系
在上述假设下,当知道时,最可能的取值为
其中的是需要进行训练的参数
在求得后,也可以将因子分析模型简记为:
其中
因子分析的损失函数与求解
因子分析的损失函数
因子分析的损失函数为最大化x的似然函数,如下:
因子分析的求解流程
因子分析的求解过程是将依次调整到L的驻点位置,相当于依次优化
但由于 的驻点与无关,所以实际上 只需调整一次,然后再依次调整即可
因子分析的求解算法主流程如下:
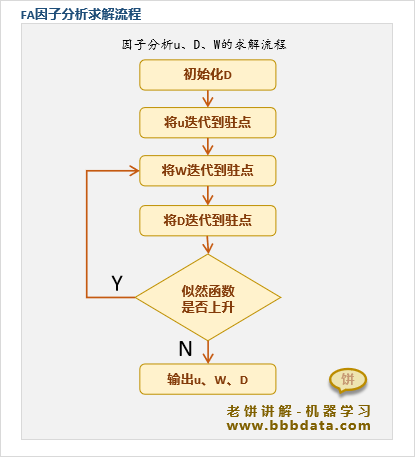
由于的驻点公式略为复杂,这里不再作展示
因子分析的具体求解及相关原理详见《》
本节展示因子分析的一个使用实例,以及代码实现
因子分析-例子解说
下面以iris鸢尾花数据为例,展示如何通过因子分析将iris的四个变量进行降维
iris鸢尾花数据如下:
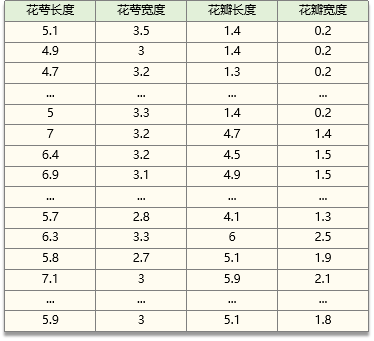
下面我们使用sklearn的FactorAnalysis来实现因子分析降维,具体代码如下:
from sklearn.decomposition import FactorAnalysis
from sklearn.datasets import load_iris
import numpy as np
import scipy
# -----训练模型-------
iris = load_iris() # 加载iris数据
X = iris.data # 用iris数据作为X
FA = FactorAnalysis() # 初始化因子分析模型
FA.fit(X) # 训练因子分析
h = FA.transform(X) # 用模型提取X的隐因子h
# -----提取模型的参数-------
W = FA.components_ # 隐变量权重
D = FA.noise_variance_ # 噪声方差
u = FA.mean_ # 阈值
A = (W/D).T@scipy.linalg.inv(np.eye(len(W)) + (W/D)@W.T) # 计算模型系数
B = -u@A # 计算模型阈值
print('\n------使用因子分析函数求解W,D,u-----')
print(' W =\n',W) # 隐变量权重
print('\n D =\n',D) # 噪声方差
print('\n u =\n',u) # 阈值
print('\n--------模型系数与阈值-----------')
print(' A =\n',A) # 模型系数
print('\n B =\n',B) # 模型阈值
print('\n 前10条数据的隐因子h=\n',h[:10,:]) # 打印隐变量(h也可以由X@A+B求得)运行结果如下:
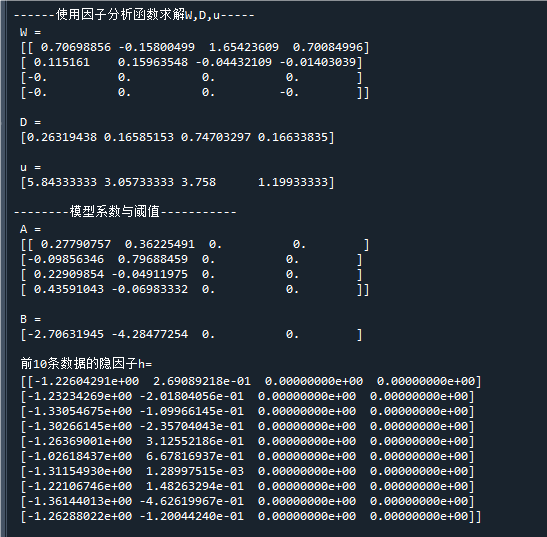
上述结果中,我们通过sklearn求得了因子分析模型中的D,W,u,
并进一步用D,W,u计算出模型的参数A,B,可知隐变量h与x的关系如下:
由于h之间是独立标准正态分布的,它的信息更为"纯粹"
因此x原本的四个变量,在h中只需两个变量就可以表示
End
 评论
评论