
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
KS分箱是一种用于对连续变量进行分箱的算法,它基于最大KS(Best-KS)切割原理,属于有监督分箱
本文讲解最大KS分箱的原理、算法流程,并通过一个案例展示KS分箱的具体过程,以及KS分箱的代码实现
通过本文,可以了解KS分箱是什么,它的分箱原理与分箱过程,以及如何用代码实现KS分箱来对连续变量进行分箱
本节介绍什么是最大KS分箱,快速了解KS分箱是什么
什么是KS分箱
KS分箱又称为最大KS分箱,它是基于KS值来对变量分箱的一种方法,属于有监督分箱
由于KS分箱基于KS,如果不了解KS是什么,可以参考文章《KS与KS曲线》
最大KS分箱是先将整体数据作为一个分箱
然后利用KS作为切割依据,不断将分箱一分为二,直到数据分为n个分箱
如下,KS分箱就是根据最大KS值所在处,将分箱不断一分为二,直到达到目标分箱个数
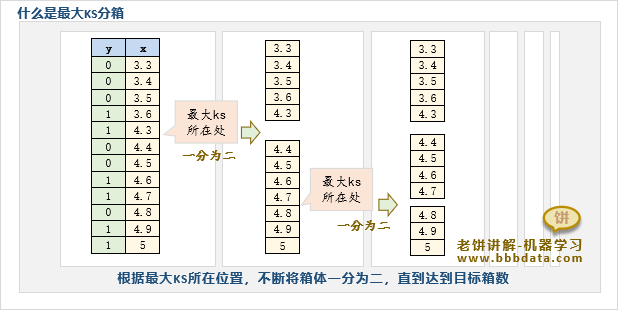
备注:由于KS分箱是基于KS值来进行分箱的一种方法,所以它只适用于二分类
本节讲解最大KS分箱的算法流程和具体细节
KS分箱-算法流程
KS分箱的算法流程如下:
1. 初始化分箱列表
初始的分箱列表,就只有一个箱[min,max]
2. 用KS进行对待分箱进行二分箱
对“待分-箱”进行最大KS二分箱,分后得到两个子箱,检验本次分箱是否有效
如果有效,将该箱分裂成两个子箱,如果无效,该箱不分裂,并标记“不需再分”
3. 判断新的分箱是否需要再分
在2中如果分裂有效,就得到两个新的子箱,判断两个子箱是否需要再分箱
如果需要继续分箱,标记为“待分”,如果不需要分箱,标记为“不需再分”
4. 检查是否达到终止条件
检查是否满足分箱终止条件,否则重复2
分箱终止条件:所有“箱”都是“不需再分-箱”,或者达到目标箱数
KS分箱中的条件判断
在主流程中,“分箱有效判断”与“判断子箱是否需要再分”的细节如下:
分箱有效的判断依据
使用KS进行分箱后,需要判断分箱是否有效
分箱是否有效的判断依据如下:
1. 子箱样本足够
如果分出的子箱样本量过少,则本次分箱无效
2. WOE方向与整体保持一致
分箱后两个子箱WOE的方向必须与整体保持一致,整体方向由第一次分箱决定
例如首次分出两箱的WOE是左大右小,则之后都要保持左大右小,否则分箱无效
WOE方向指的是判断,其中:
备注:由于只是比较左右WOE的大小,所以可以只比较内部的好坏比就可以
即判断 就可以得到
判断子箱是否需要再分的依据
在KS分箱流程中,将分箱一分为二后,得到两个子箱
子箱是否需要再分的判断依据如下:
1. 箱内全是同一类:如果全是同一类,则不需要再分
2. 箱内样本量过少:如果箱内样本量过少,则不需要再分
本节通过一个具体的实例,一步一步解说KS分箱是如何执行的
KS实例解说-问题与数据
以breast_cancer里的数据第一个变量为例,讲解如何进行KS分箱
数据如下:
其中,x为breast_cancer的第一个变量
下面使用最大KS分箱法对x进行分箱,
目标是:最大分箱不超过6个,且每个分箱样本不低于20个
KS实例解说-分箱过程
用最大KS分箱法对x进行分箱的具体过程如下:
一、初始分箱
初始分箱只有一个,就是[min(x),max(x)] = [6.981, 28.11]
由于分箱的样式统一为(a,b],我们不妨将6.981向下截取一点
因此,最终得到初始分箱为:init_bin = (6.881, 28.11]
二、对初始分箱进行KS二分箱
如图所示,先求切割点,再判断切割是否有效,如果有效则将箱一分为二
1. 先求切割点
取出初始分箱的数据(即6.881<x<=28.11 的样本)
求取初始分箱数据的最大KS点对应的x, 这里求得x为14.99
以14.99为切割点,将箱体一分为二,得到两个子箱:(6.881,14.99 ],(14.99,28.11]
2. 判断切割是否有效
(1) 判断子箱样本是否足够
左箱有395个样本,右箱有174个样本,结论:足够
(2) 判断woe方向是否正确
左箱坏样本个数/左箱好样本个数= 344/51 = 6.74
右箱坏样本个数/右箱好样本个数= 13/161 = 0.08
6.74> 0.08 ,左箱woe>右箱woe ,故woe方向为下降
由于本次是第一次分箱,不需要判断woe方向是否满足
但需要记录下本次的woe方向,之后的分箱要与此保持一致
结论:样本量足够,且woe方向满足,本次分箱有效
3. 将箱一分为二,得到(6.881,14.99 ],(14.99,28.11]
三、判断新分箱是否需要再分

1. 判断左箱(6.881,14.99 ]是否需要再分
(1)判断样本是否足够:左箱有395个样本,样本足够
(2)判断是否全为一类:好坏样本分别为344和51,未全为好或坏
结论:左箱需要继续分箱
2. 判断右箱(14.99,28.11]是否需要再分
(1)判断样本是否足够 :左箱有174个样本,样本足够
(2)判断是否全为一类:好坏样本分别为13和161,未全为好或坏
结论:右箱需要继续分箱
四、判断是否终止分箱
判断是否要终止分箱:
1. 是否有待分箱:当前还有两个分箱需要分
2. 箱数是否足够:当前只有两够分箱,未达到最大箱数
结论:继续分箱
五、继续重复分箱
继续对(6.881,14.99 ]进行分箱......
如此循环.......
整个分箱过程如下:
最后得到分箱结果如下:
本节展示如何用代码实现KS分箱,用于对变量进行自动分箱
最大KS分箱代码
目前python没有很统一使用的KS分箱的包,更多的是自己实现
下面用python实现KS分箱,它只适用于连续变量与二分类标签
具体代码实现如下:
# -*- coding: utf-8 -*-
"""
最大KS分箱的代码实现和Demo
本代码由《老饼讲解-机器学习》www.bbbdata.com编写
"""
from sklearn.metrics import roc_curve
import numpy as np
from sklearn.datasets import load_breast_cancer
import pandas as pd
# 将类别转为类别矩阵(one-hot格式)
def class2Cmat(y):
c_name = list(np.unique(y)) # 类别名称
c_num = len(c_name) # 类别个数
cMat = np.zeros([len(y),c_num]) # 初始化类别矩阵
for i in range(c_num):
cMat[y==c_name[i],i] = 1 # 将样本对应的类别标为1
c_name = [str(i) for i in c_name] # 类别名称统一转为字符串类型
return cMat,c_name # 返回one-hot类别矩阵和类别名称
# 将切割点转换成分箱说明
def getBinDesc(bin_cut):
# 分箱说明
bin_first = ['<='+str(bin_cut[0])] # 第一个分箱
bin_last = ['>'+str(bin_cut[-1])] # 最后一个分箱
bin_desc = ['('+str(bin_cut[i])+','+str(bin_cut[i+1])+']' for i in range(len(bin_cut)-1)]
bin_desc = bin_first+bin_desc+bin_last # 分箱说明
return bin_desc
# 计算分箱详情
def statBinNum(x,y,bin_cut):
if(len(bin_cut)==0): # 如果没有切割点
return None # 返回空
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
c_mat,c_name = class2Cmat(y) # 将类别转为one-hot类别矩阵
df = pd.DataFrame(c_mat,columns=c_name,dtype=int) # 将类别矩阵转为dataFrame
df['cn'] = 1 # 预设一列1,方向后面统计
df['grp'] = 0 # 初始化分组序号
df['grp_desc'] = '' # 初始化分箱说明
# 计算各个样本的分组序号与分箱说明
df.loc[x<=bin_cut[0],'grp']=0 # 第0组样本的序号
df.loc[x<=bin_cut[0],'grp_desc'] =bin_desc[0] # 第0组样本的分箱说明
for i in range(len(bin_cut)-1): # 逐区间计算分箱序号与分箱说明
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp'] =i+1
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp_desc'] =bin_desc[i+1]
df.loc[x>bin_cut[-1],'grp']=len(bin_cut) # 最后一组样本的序号
df.loc[x>bin_cut[-1],'grp_desc']=bin_desc[-1] # 最后一组样本的分箱说明
# 按组号聚合,统计出每组的总样本个数和各类别的样本个数
col_dict = {'grp':'max','grp_desc':'max','cn':'sum'}
col_dict.update({col:'sum' for col in c_name})
df = df.groupby('grp').agg(col_dict).reset_index(drop=True)
return df
#---------------------以上部分只用于统计分箱结果详情,与KS分箱算法无关-----------------------
# 获取ks切割点
def getKsCutPoint(x,y):
fpr, tpr, thresholds= roc_curve(y, x) # 计算fpr,tpr
ks_idx = np.argmax(abs(fpr-tpr)) # 计算最大ks所在位置
#由于roc_curve给出的切割点是>=作为右箱,而我们需要的是>作为右箱,所以切割点应向下再取一位,也即索引向上取一位
return thresholds[ks_idx+1] # 返回切割点
# 检查切割点是否有效
def checkCutValid(x,y,cutPoint,woe_asc,min_sample):
left_y = y[x<=cutPoint] # 左箱的y
right_y = y[x>cutPoint] # 右箱的y
check_sample_num = min(len(left_y),len(right_y))>=min_sample # 检查左右箱样本是否足够
left_rate = sum(left_y)/max((len(left_y)-sum(left_y)),1) # 左箱好坏比例
right_rate = sum(right_y)/max((len(right_y)-sum(right_y)),1) # 右箱好坏比例
cur_woe_asc = left_rate<right_rate # 通过好坏比例的比较,确定woe是否上升
check_woe_asc = True if woe_asc ==None else cur_woe_asc == woe_asc # 检查woe方向是否与预期一致
woe_asc = cur_woe_asc if woe_asc ==None else woe_asc # 首次woe方向为空,需要返回woe方向
cut_valid = check_sample_num & check_woe_asc # 样本足够且woe方向正确,则本次切割有效
return cut_valid,woe_asc
# 获取箱体切割点
def cutBin(bin_x,bin_y,woe_asc,min_sample):
cutPoint = getKsCutPoint(bin_x,bin_y) # 获取最大KS切割点
is_cut_valid,woe_asc = checkCutValid(bin_x,bin_y,cutPoint,woe_asc,min_sample) # 检查切割点是否有效
if( not is_cut_valid): # 如果切割点无效
cutPoint = None # 返回None
return cutPoint,woe_asc # 返回切割点
# 检查箱体是否不需再分
def checkBinFinish(y,min_sample):
check_sample_num = len(y)<min_sample # 检查样本是否足够
check_class_pure = (sum(y) == len(y))| (sum(y) == 0) # 检查样本是否全为一类
bin_finish = check_sample_num | check_class_pure # 如果样本足够或者全为一类,则不需再分
return bin_finish
# KS分箱主流程
def ksMerge(x,y,min_sample,max_bin):
# -----初始化分箱列表等变量----------------
un_cut_bins = [[min(x)-0.1,max(x)]] # 初始化待分箱列表
finish_bins = [] # 初始化已完成分箱列表
woe_asc = None # 初始化woe方向
# -----如果待分箱体不为空,则对待分箱进行分箱----------------
for i in range(10000): # 为避免有bug使用while不安全,改为for
cur_bin = un_cut_bins.pop(0) # 从待分箱列表获取一个分箱
bin_x = x[(x>cur_bin[0])&(x<=cur_bin[1])] # 当前分箱的x
bin_y = y[(x>cur_bin[0])&(x<=cur_bin[1])] # 当前分箱的y
cutPoint,woe_asc = cutBin(bin_x,bin_y,woe_asc,min_sample) # 获取分箱的最大KS切割点
if (cutPoint==None): # 如果切割点无效
finish_bins.append(cur_bin) # 将当前箱移到已完成列表
else: # 如果切割点有效
# ------检查左箱是否需要再分,需要再分就添加到待分箱列表,否则添加到已完成列表-----
left_bin = [cur_bin[0],cutPoint] # 生成左分箱
left_y = bin_y[bin_x <=cutPoint] # 获取左箱y数据
left_finish = checkBinFinish(left_y,min_sample) # 检查左箱是否不需再分
if (left_finish): # 如果左箱不需再分
finish_bins.append(left_bin) # 将左箱添加到已完成列表
else: # 否则
un_cut_bins.append(left_bin) # 将左箱移到待分箱列表
# ------检查右箱是否需要再分,需要再分就添加到待分箱列表,否则添加到已完成列表-----
right_bin = [cutPoint,cur_bin[1]] # 生成右分箱
right_y = bin_y[bin_x >cutPoint] # 获取右箱y数据
right_finish = checkBinFinish(right_y,min_sample) # 检查右箱是否不需再分
if (right_finish): # 如果右箱不需再分
finish_bins.append(right_bin) # 将右箱添加到已完成列表
else: # 否则
un_cut_bins.append(right_bin) # 将右箱移到待分箱列表
# 检查是否满足退出分箱条件:待分箱列表为空或者分箱数据足够
if((len(un_cut_bins)==0)|((len(un_cut_bins)+len(finish_bins))>=max_bin)):
break
# ------获取分箱切割点-------
bins = un_cut_bins + finish_bins # 将完成或待分的分箱一起作为最后的分箱结果
bin_cut = [cur_bin[1] for cur_bin in bins] # 获取分箱右边的值
list.sort(bin_cut) # 排序
bin_cut.pop(-1) # 去掉最后一个,就是分箱切割点
# ------------分箱说明--------------
bin_desc ='['+str(min(x))+','+str(max(x))+']' # 如果没有切割点,就只有一个分箱[min_x,max_x]
if (len(bin_cut)>0) : # 如果有切割点
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
# ------------返回结果--------------
return bin_cut,bin_desc
#----------使用Demo----------------------------------
# 数据加载
breast = load_breast_cancer()
x = breast.data[:,0]
y = breast.target
# KS分箱
bin_cut,bin_desc = ksMerge(x,y,min_sample=19,max_bin=6) # 进行KS分箱,
bin_stat = statBinNum(x,y,bin_cut) # 计算各个分箱的样本个数
# 打印结果
print('切割点:' ,bin_cut)
print('分箱说明:',bin_desc)
print('---------分箱统计----------')
print(bin_stat)代码运行结果如下:
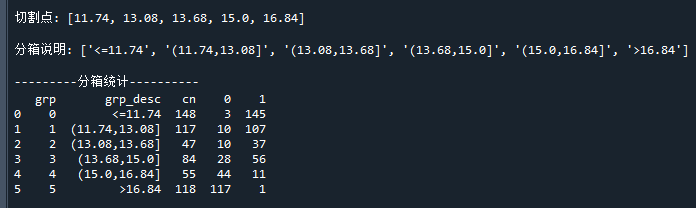
可以看到,最大KS分箱通过5个切割点,把变量分为了6个箱
好了,以上就是KS分箱的原理和代码实现了~
End
 评论
评论