
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
过拟合是RBF神经网络需要解决的核心问题之一,减少径向基个数可以有效抑制RBF神经网络过拟合
本文展示一个具体的实验例子来说明径向基过多为什么会引起RBF神经网络的过拟合,并剖析其中的原因
通过本文,可以加深理解径向基个数对RBF神经网络泛化能力的影响,和如何减少径向基来抑制RBF神经网络过拟合
本节讲解为什么通过减少RBF个数可以抑制RBF神经网络过拟合,以及newrb函数中减少RBF个数的方法
通过减少径向基个数抑制RBF网络过拟合
在使用RBF神经网络建模时,抑制模型过拟合,增加模型的泛化能力是核心问题之一
而减少径向基个数就是一种有效抑制RBF网络过拟合的手段
过拟合的内部表现就是模型起伏跌宕,越多的径向基,意味着模型越有能力跌宕
可以想象一下,两个径向基可以叠加出双峰曲线,但不可能拟合出多峰曲线
所以RBF网络拟合出来的曲线十分路宕的前提就是有足够多的径向基
因此,我们可以通过减少径向基个数,削弱它的跌宕能力,使得网络更为平滑,从而达到抑制过拟合
在newrb中减少径向基个数的方法
newrb函数的完整入参如下
net = newrb(P,T,goal,spread,MN,DF)
我们知道,newrb使用的是OLS求解法,它在构建过程中逐个把径向基添加到网络中
在spread固定的情况下,newrb函数中共有两个参数控制了径向基的个数:
👉1.MN:RBF网络的径向基个数>MN时就不再添加径向基
👉2.goal:参RBF网络的误差<=goal时就不再添加径向基
可以用MN来强行设定径向基的个数,但实际中,往往使用goal会更加贴切使用需求
本节通过一个实验案例,来加深理解减少径向基个数是如何抑制RBF网络过拟合的
调整径向基个数解决RBF过拟合-案例分析
问题:spread设置足够大的情况下仍然过拟合
现有数据点如下:
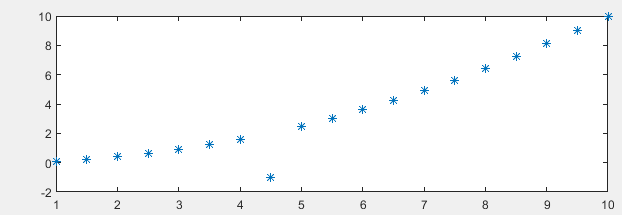
我们使用RBF径向基神经网络拟合如下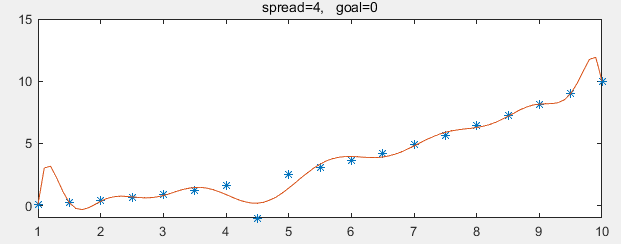
可以看到,曲线是弯弯曲曲,在两端的两个小突坡更是明显不合理的
这样的网络的预测效果就会不太理想,特别是两端的小突坡位置
备注:可以注意到,此时的spread已经是足够大的,
因为goal为0但却无法拟合所有数据点(也就是spread已经大到出现数值问题了)
解决方案:通过减少径向基个数来抑制RBF神经网络过拟合
在上述案例中,spread已经设置足够大了,但RBF网络仍然明显过拟合
那么,此时就可以通过减少径向基的个数来削弱网络的跌宕能力,使最终的曲线更加平滑
在上述例子中,一共用了19个径向基,
此时,我们不妨放宽训练误差,将goal设为2,RBF网络最终只用了2个RBF,效果如下:
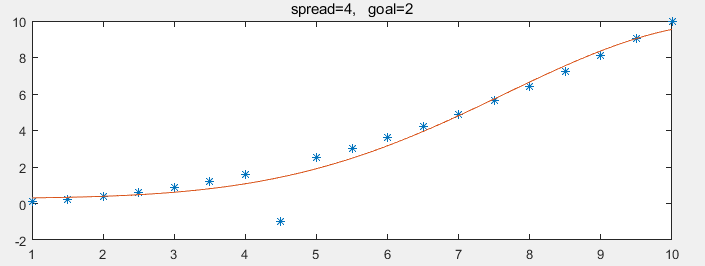
可以看到,RBF网络要平滑了许多,已经有效地抑制过拟合网络的过拟合
网络最终只用了2个RBF,这相当于强行限制了RBF的跌宕上限,从而减缓了网络的过拟合
实验代码
上述实验中所用到的代码如下:
clear all
close all
%代码说明:通过调整RBF神经网络的隐节点个数来避免过拟合的实验代码
%来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2018a
%-----------------------------------------------------
% ----数据生成-----
x = 1:0.5:10; % 生成数据点x
y = x.*x/10; % 生成数据点y
y(8) = -1; % 为特殊构造数据,这里将y的第8个数据改为-1
% ----参数设置与网络训练-----
spread = 4; % spread
goal = 2; % goal的设定,在实验中分为别为0和2
net = newrb(x, y,goal,spread); % 用当前spread构建网络
% ----绘制结果-----
t = 1:0.1:10; % 用于画线的x
ty = t.*t/10; % 用于画线的y
simt = sim(net,t); % 计算网络的曲线值
plot(x,y,'*',t,simt) % 绘制网络曲线
title(['spread=',num2str(spread),', goal=',num2str(goal)])
hn = size(net.lw{2,1},2) % 隐节点(径向基)个数好了,以上就是如何通过减少径向基个数来解决RBF过拟合的方法了~
End