
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
MLP神经网络往往也称为BP神经网络,因为它在计算梯度时使用的是BP算法
本文讲解如何使用BP算法计算MLP神经网络的梯度,并展示具体算法流程与实现例子
通过本文,可以了解MLP神经网络的梯度是如何计算的,以及MLP梯度计算的代码实现
本节讲解MLP神经网络是如何利用BP算法计算参数梯度的
MLP与MLP的梯度计算方法
MLP神经网络是一种前馈神经网络,它由多层构成,每层的输出是下层的输入
由于MLP往往使用梯度下降、动量梯度下降等算法进行训练,因此需要计算MLP模型里的参数梯度
MLP神经网络的梯度计算思路如下:
由于MLP的损失函数为单样本的损失函数的均值,即
因此,损失函数的梯度也是单样本梯度的均值:
如果将单个样本的损失函数设为,则梯度就是单个样本梯度之和:
这里的是样本个数,则代表MLP神经网络的任意一个权重或阈值
因此,对于MLP,只需计算单个样本损失函数的梯度,再取均值(或取和)就可得到总的梯度
MLP的梯度计算方法一般如下:
如图所示,MLP的梯度计算一般先通过BP算法,逐层从后往前计算单样本的梯度
在计算完每层所有样本的梯度时,就进行求和,从而得到该层参数W、B的整体梯度
MLP的单样本梯度计算
MLP单样本的梯度一般使用BP算法来计算,BP算法从最后一层开始,后馈式计算梯度
BP算法的流程
BP算法先计算当层的输出梯度,再通过输出梯度进一步计算该层的参数梯度
设MLP共有K个计算层,BP算法的过程如下:
1. 计算第K层(即最后一层)的输出梯度
2. 计算第K层的参数梯度
3. 计算第K-1层的输出梯度
4. 计算第K-1层的参数梯度
....
如此类推,直到第一层,即可算得所有层的参数
总的来说,BP算法就是从最后一层开始,先算出当层输出的梯度,再计算当层的参数梯度,直到第一层
MLP梯度计算公式
MLP每层的输出梯度、参数梯度公式如下:
一、输出梯度
1. 设单个样本的损失函数为均方差函数MSE:
则最后一层(第K层)的输出梯度为:
2. 其余层的输出梯度依赖于后层的输出梯度
第k-1层的输出梯度为:
二、参数梯度
第k层的权重、阈值的梯度都依赖于第k层输出的梯度,计算公式如下:
第k层的权重梯度:
第k层的阈值梯度:
激活函数的梯度
其中,当激活函数T=tanh时,根据tanh函数的导数,有:
当没有激活函数时,可以认为激活函数是恒等函数 ,则有:
本节推导MLP线性层的输出梯度与参数梯度
MLP最后一层输出的梯度公式-推导
最后一层的输出梯度公式推导
对于单个样本,不妨设损失函数为均方差函数MSE,则损失函数为:
这里M是样本个数,N是MLP的输出个数,是最后一层(第K层)的第i个输出值,是真实值
则对于最后一层的第个输出,它的梯度为:
按形式进行推广,即可得到最后一层所有输出的梯度为:
其余层的输出梯度公式推导
MLP每层都为线性层,它的前馈公式为:
,T为激活函数
由于MLP每层的输出就是后层的输入,因此只需求出线性层的输入梯度
推导过程如下:
1. 线性层第j个输出对第i个输入的梯度为:
2. 按形式进行推广,即可得到线性层所有输出对第i个输入的梯度向量:
3. 因此,损失函数对线性层的第i个输入的梯度为:
4. 按形式进行推广,即可得到损失函数对所有输入的梯度向量为:
线性层对输入、权重w、阈值b的梯度
MLP每层都为线性层,它的前馈公式为:
,T为激活函数
它的权重、阈值的梯度公式如下
权重W的梯度
线性层的权重W的梯度推导过程如下:
1. 线性层第j个输出对单个权重参数的梯度为:
2. 由上可知,是一个第u个元素为,其余为0的向量
因此,损失函数对线性层的单个权重的梯度为:
3. 按形式进行推广,则损失函数对线性层的整个W的梯度为:
阈值b的梯度
线性层的权重W的梯度推导过程如下:
1. 线性层第j个输出对单个阈值参数的梯度为:
2. 由上可知,即是一个第u个元素为,其余为0的向量
因此,损失函数对线性层的第u个阈值的梯度为:
3. 按形式进行推广,则损失函数对线性层的整个的梯度为:
本节讲解MLP神经网络梯度计算的算法流程
MLP的梯度计算
MLP采用BP算法来计算单个样本的参数梯度,再进行求和,就是总梯度
MLP计算梯度的算法流程图如下:
一、前馈
通过前馈计算,获得每层的输入与输出:
将第一层的输入进行前馈,得到:
备注:通过前馈就得到了各层的输出,同时也就得到了各层的输入
进行前馈,是因为在后馈时需要使用各层的输出输入来计算梯度
二、后馈
1. 初始化最后一层的输出梯度
直接计算损失函数对于最后一层输出的梯度:
2. 逐层后馈
从最后一层开始逐层前馈,对于第k层有:
2.1. 计算当前层权重、阈值的梯度:
计算各个样本的权重、阈值梯度,并求和,得到总梯度
设当前层为第k层,其权重、阈值的梯度公式如下:
备注:阈值中的sum是对每行求和,权重梯度已是求和结果,不需sum,下文详细解说
2.2. 计算当前层输入的梯度:
备注:第k层输入入的梯度,也就是第k-1层的输出梯度
即:
总的来说,BP算法就是从最后一层开始,每层算出当层的参数梯度和输入梯度(即前层输出梯度),直到第一层
关于W的梯度求和
由于W是一个矩阵,它的单样本梯度公式也是一个矩阵
因此,它并不能直接由梯度公式进行批量计算,而需要一个一个样本计算
即如得到各个样本的权重梯度后,再进行求和
这样是低效的,因此,W的计算方法如下:
由于对单个样本有:
其中是一个列向量,是行向量
就是的第个元素乘以的第个元素
而对于整体样本,则是一个矩阵,每列代表一个样本,第行代表一个样本
因此,所有样本的梯度之和就是的第行与的第列对应元素相乘再求和
即:
从而对整体样本,W的梯度为:
即:
因此,W在单样本时,按该公式求得的是单样本的梯度,在多样本时,求得的是梯度之和
本节展示如何使用代码实现MLP神经网络的梯度计算
MLP梯度计算-代码实现
下面按照上述BP算法流程与公式,实现一个MLP神经网络的梯度计算
具体代码如下:
# 本代码用于展示如何使用BP算法计算MLP神经网络的梯度
# 本代码来自《老饼讲解-深度学习》 www.bbbdata.com
import numpy as np
#----------------自写代码计算MLP神经网络的梯度--------------------
# 将层定义为类对象
class Layer:
def __init__(self, w,b,activeFcn):
self.w = w # 该层的权重参数
self.b = b # 该层的阈值参数
self.y = None # 该层的输出
self.x = None # 该层的输入
self.dw = None # 该层的参数梯度
self.db = None
self.dx = None # 该层的输入梯度
self.activeFcn= activeFcn # 该层的激活函数
def forward(self,x):
self.x = x # 更新输入
self.y = self.w@x+self.b # 激活前的值
if (self.activeFcn=='tanh') : # 如果是tanh激活函数
self.y = np.tanh(self.y) # 按tanh激活
elif(self.activeFcn==None) : # 如果没有激活函数,则按原值
self.y = self.y
def backward(self,dy):
if (self.activeFcn=='tanh') : # 如果是tanh激活函数
dA = (1-self.y**2) # 计算tanh激活函数的梯度
elif(self.activeFcn==None) : # 如果没有激活函数
dA = np.ones(self.y.shape) # 则梯度全为1
self.dw = (dA*dy)@self.x.T # 计算权重w的梯度
self.db = (dA*dy).sum(axis=1) # 计算阈值的梯度
self.dx = self.w.T@(dy*dA) # 计算输入的梯度
# 初始化一个MLP神经网络
w1= np.ones([3,2])*0.1 # 初始化权重w1
b1= np.ones([3,1])*0.1 # 初始化阈值b1
w2= np.ones([3,3])*0.1 # 初始化权重w2
b2= np.ones([3,1])*0.1 # 初始化阈值b2
w3= np.ones([2,3])*0.1 # 初始化权重w3
b3= np.ones([2,1])*0.1 # 初始化阈值b4
layers = [Layer(w1,b1,'tanh'),Layer(w2,b2,'tanh'),Layer(w3,b3,None)] # 初始化前馈网络
x = np.array([[3.,2.],[4,5]]) # 样本的x
y = np.array([[2.,1.],[2.,2.]]) # 样本的y
# --------BP算法计算梯度-----------------
# 先通过前馈来计算出每层的输出
for i in range(len(layers)): # 逐层前馈
layers[i].forward(x) # 计算当前层的输出
x = layers[i].y # 当将前层的输出作为下层输入
# 后馈计算梯度
y_pred = layers[-1].y # 最后一层的输出就是预测值
dy = 2*(y_pred - y)/(y.shape[0]*y.shape[1]) # 最后一层输出的梯度
for i in range(len(layers)-1,-1,-1): # 从最后一层开始计算梯度
layers[i].backward(dy) # 计算当前层的梯度
dy = layers[i].dx # 将当前层传播给输入的梯度,作为下层输出的梯度
# 打印结果
print('\n----自写代码计算MLP神经网络的梯度----:')
for i in range(len(layers)):
print('第',str(i),'层权重w梯度:',layers[i].dw) # 打印每层的参数梯度
print('第',str(i),'层阈值b梯度:',layers[i].db) # 打印每层的参数梯度
# ----------------使用pytorch计算梯度-------------------------
import torch
x = torch.tensor([[3.0,2.0],[4.0,5.0]],dtype=(float)) # 样本的x
y = torch.tensor([[2.,1.],[2.,2.]],dtype=(float)) # 样本的y
w1= torch.full((3,2),0.1,dtype=(float),requires_grad=True) # 初始化权重w1
b1= torch.full((3,1),0.1,dtype=(float),requires_grad=True) # 初始化阈值b1
w2= torch.full((3,3),0.1,dtype=(float),requires_grad=True) # 初始化权重w2
b2= torch.full((3,1),0.1,dtype=(float),requires_grad=True) # 初始化阈值b2
w3= torch.full((2,3),0.1,dtype=(float),requires_grad=True) # 初始化权重w3
b3= torch.full((2,1),0.1,dtype=(float),requires_grad=True) # 初始化阈值b3
output = w3@torch.tanh(w2@torch.tanh(w1@x+b1)+b2)+b3 # 根据x计算输出
loss = sum(sum(((output - y)**2)))/(y.shape[0]*y.shape[1]) # 计算损失值
loss.backward() # 将loss反向传播
print('\n----pytorch计算MLP神经网络的梯度----:')
print('w1的梯度:',w1.grad) # 打印loss对w的梯度
print('b1的梯度:',b1.grad) # 打印loss对w的梯度
print('w2的梯度:',w2.grad) # 打印loss对w的梯度
print('b2的梯度:',b2.grad) # 打印loss对w的梯度
print('w3的梯度:',w3.grad) # 打印loss对w的梯度
print('b3的梯度:',b3.grad) # 打印loss对w的梯度代码运行结果如下:
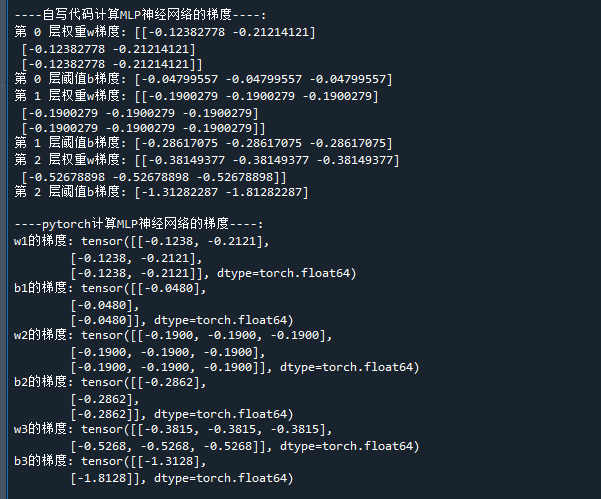
在本代码中,我们同时使用了pytorch的自动求导
通过结果,可以看到,自写代码实现的MLP神经网络梯度计算结果与pytorch的是一致的
好了,以上就是MLP神经网络的梯度计算方法与代码实现了~
End
 评论
评论