
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
卡方分箱是一种基于卡方独立检验的、利用卡方值对变量进行分箱的方法
本文讲解卡方分箱的算法流程,并通过一个具体例子展示卡方分箱是如何一步一步分箱的
通过本文,可以快速了解卡方分箱是什么、卡方分箱原理、流程,以及卡方分箱的具体代码实现
本节展示什么是卡方分箱,以及它的用途
什么是卡方分箱
卡方分箱是基于卡方独立检验、利用卡方值对连续变量进行变量分箱的一种方法
由于卡方分箱是基于卡方独立检验的,如果不熟悉的可以参考文章《卡方检验-独立检验》
卡方分箱的方法如下:
卡方分箱先初始化m个分箱,然后不断合并分箱,直到分箱数只剩n个
每次合并分箱时,它用卡方值判断哪两个相邻分箱的类别分布最没区分度,就合并哪两个分箱
如图,卡方分箱先初始化多个分箱,然后根据卡方值来不断进行合并,直到只剩目标分箱个数
备注:卡方分箱原论文:https://sci2s.ugr.es/keel/pdf/algorithm/congreso/1992-Kerber-ChimErge-AAAI92.pdf
卡方分箱-算法流程
卡方分箱的流程如下:
一、初始化分箱
将变量先初始化分为m个箱
初始化分箱可以等距、等频或其它规则进行初始化
二、计算相邻箱的卡方值
相邻箱的卡方值:即两个分箱对y的响应是否独立的评估
三、合并分箱
找出卡方值最小值的一组相邻箱,将其合并
即合并最不独立的两个邻箱
四、判断分箱终止条件
判断是否满足停止条件,如是,则停止,否则重复2-4
停止条件一般可设为:箱数小于目标箱数m
五、输出
输出最终的分箱结果,以及相邻箱的p值
上述流程涉及卡方值和p值的计算,下面是它们的计算方法
(这里仅简要列出流程,其原理请参考《卡方独立检验》)
设当前的两个分箱为与 ,现用代表分箱里类别的样本个数
然后按如下流程计算卡方值与P值:
一、计算期望值
其中,为第i行求和,为第j列求和, 为总样本数
二、根据公式计算卡方值
卡方值的计算公式如下:
三、卡方值转换为P值
1. 确定自由度DF
r 为A的行数, c 为A的列数
2. 根据卡方概率分布积分函数计算p值
是自由度为DF的卡方概率累计分布函数,它的计算通常由程序给出
本节以具体数据为例,展示卡方分箱是如何一步一步进行分箱的
卡方分箱过程-实例解说
iris数据的sepal_length变量与类别的数据如下:
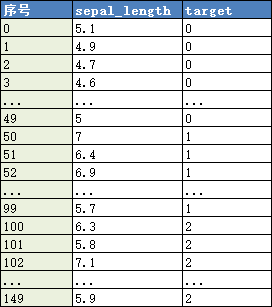
我们希望使用卡方分箱,将sepal_length分成5个箱
卡方分箱的过程如下:
一、初始化分箱
先初始化分箱,我们这里将它初始化成10个分箱
初始化分箱可以等距、等频分箱或其它规则初始化分箱
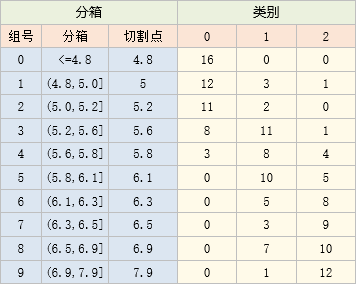
以第一行为例,它代表 x <=4.8时,0、1、2类别各有16、0、0个
这里统计类别个数,主要是为了方便后面计算卡方值
二、计算卡方值(计算相邻两个分箱的卡方值)
分别计算相邻两个分箱(0与1、1与2.....8与9)的卡方值,结果如下:
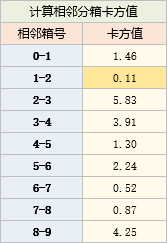
三、合并分箱
将卡方值最小的两个分箱合并
根据2中结果,卡方值最小的是1号箱与2号箱
将1号箱与2号箱合并,并重置箱号,得到新的分箱表:
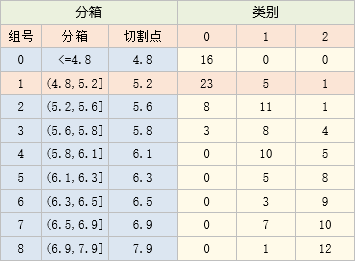
四、 最终分箱结果
重复以上步骤,直到达到分箱终止条件
重复二、三步,直到箱数等于目标箱数5,则停止
最终结果如下:
我们可以看到,最后分箱结果中,0 号箱基本是0类
1、2号箱偏向1类 ,3、4号箱偏向2类,说明得到了较好的分箱效果
五、计算p值
我们还可以计算相邻分箱的p值
p值越小,代表区分越明显,p值越大,代表分箱越没区分度
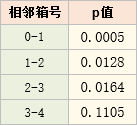
根据上面的P值列表,可以考虑将 3-4箱合并,因为P值较大
卡方值、P值计算实例
上面例子涉及到卡方值和p值的计算,这里详细讲解卡方值和p值是怎么算出来的
以上述例子中,4号箱与5号箱数据:
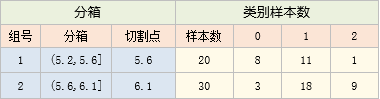
以其为例,计算卡方值的过程如下:
一、行列分别求和
二、计算期望值
三、根据公式计算卡方值
四、卡方值转换p值
先计算自由度DF,如下:
把卡方值代入下式,即可得到p值
,其中,是自由度为2的卡方累计分布函数
卡方累计分布函数需要查表或用程序计算,在python中可以如下计算:
1-scipy.stats.chi2.cdf(df=2, x=8.7108)

即可得到:p = 0.0128373
本节展示卡方分箱的具体代码实现
卡方分箱-代码实现
下面用python实现卡方分箱,它只适用于连续变量
具体代码实现如下:
# -*- coding: utf-8 -*-
"""
卡方分箱的代码实现和Demo
本代码由《老饼讲解-机器学习》www.bbbdata.com编写
"""
import numpy as np
from sklearn.datasets import load_iris
import pandas as pd
import scipy
# 将类别转为类别矩阵(one-hot格式)
def class2Cmat(y):
c_name = list(np.unique(y)) # 类别名称
c_num = len(c_name) # 类别个数
cMat = np.zeros([len(y),c_num]) # 初始化类别矩阵
for i in range(c_num):
cMat[y==c_name[i],i] = 1 # 将样本对应的类别标为1
c_name = [str(i) for i in c_name] # 类别名称统一转为字符串类型
return cMat,c_name # 返回one-hot类别矩阵和类别名称
# 将切割点转换成分箱说明
def getBinDesc(bin_cut):
# 分箱说明
bin_first = ['<='+str(bin_cut[0])] # 第一个分箱
bin_last = ['>'+str(bin_cut[-1])] # 最后一个分箱
bin_desc = ['('+str(bin_cut[i])+','+str(bin_cut[i+1])+']' for i in range(len(bin_cut)-1)]
bin_desc = bin_first+bin_desc+bin_last # 分箱说明
return bin_desc
# 计算分箱详情
def statBinNum(x,y,bin_cut):
if(len(bin_cut)==0): # 如果没有切割点
return None # 返回空
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
c_mat,c_name = class2Cmat(y) # 将类别转为one-hot类别矩阵
df = pd.DataFrame(c_mat,columns=c_name,dtype=int) # 将类别矩阵转为dataFrame
df['cn'] = 1 # 预设一列1,方向后面统计
df['grp'] = 0 # 初始化分组序号
df['grp_desc'] = '' # 初始化分箱说明
# 计算各个样本的分组序号与分箱说明
df.loc[x<=bin_cut[0],'grp']=0 # 第0组样本的序号
df.loc[x<=bin_cut[0],'grp_desc'] =bin_desc[0] # 第0组样本的分箱说明
for i in range(len(bin_cut)-1): # 逐区间计算分箱序号与分箱说明
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp'] =i+1
df.loc[(x>bin_cut[i])&(x<=bin_cut[i+1]),'grp_desc'] =bin_desc[i+1]
df.loc[x>bin_cut[-1],'grp']=len(bin_cut) # 最后一组样本的序号
df.loc[x>bin_cut[-1],'grp_desc']=bin_desc[-1] # 最后一组样本的分箱说明
# 按组号聚合,统计出每组的总样本个数和各类别的样本个数
col_dict = {'grp':'max','grp_desc':'max','cn':'sum'}
col_dict.update({col:'sum' for col in c_name})
df = df.groupby('grp').agg(col_dict).reset_index(drop=True)
return df
# 初始化分箱
'''
按等频分箱,等频分箱并不代表每个箱里的样本个数都一样,
因为如果每10个样本作为一个箱,刚好9-11样本的x取值一样,
那必须把9-11划到同一个箱。
'''
def initBin(x,y,bin_num=10):
xx = x.copy()
xx.sort()
idx = [int(np.floor((len(x)/bin_num)*(i+1))-1) for i in range(bin_num-1)]
bin_cut = list(xx[idx])
return bin_cut
#计算卡方值
def cal_chi2(pair):
# chi2_value,p,free_n,ex = scipy.stats.chi2_contingency(pair)
pair[pair==0] = 1
class_rate = pair.sum(axis=1)/pair.sum().sum() # 两类样本的占比
col_sum = pair.sum(axis=0) # 各组别的样本个数
ex = np.dot(np.array([class_rate]).T,np.array([col_sum])) # 计算期望值
chi2 = (((pair - ex)**2/ex)).sum() # 计算卡方值
return chi2
# 计算P值
def cal_p(df):
chi2_list = [cal_chi2(np.array(df.iloc[i:i+2,:])) for i in range(df.shape[0]-1)] # 计算卡方值
grp_num = df.shape[1] # 计算组别个数
free_n = grp_num - 1 # 计算自由度
p_list = [1-scipy.stats.chi2.cdf(df=free_n, x=i) for i in chi2_list] # 计算p值
return p_list
# 卡方分箱主函数,bin_desc为分组说明
def Chi2Merge(x,y,bin_num = 5,init_bin_num=10):
# ------------初始化--------------------------------
bin_cut = initBin(x,y,bin_num=init_bin_num) # 初始化分箱
df = statBinNum(x,y,bin_cut)
df.drop(columns = ['cn'])
bin_cut.append(max(x))
df['grp_desc'] = bin_cut
c_name = list(np.unique(y))
c_name = [str(i) for i in c_name]
# ------------根据卡方值合并分箱,直到达到目标分箱数---------------------
while(df.shape[0]>bin_num):
# 计算卡方值
chi2_list = [cal_chi2(np.array(df[c_name][i:i+2])) for i in range(df.shape[0]-1)]
#将卡方值最小的两组合并
min_idx = np.argmin(chi2_list)
df.loc[min_idx+1,c_name] += df.loc[min_idx,c_name]
df.drop(min_idx, inplace = True)
df = df.reset_index(drop=True)
# ----------输出结果-----------------------------
bin_cut = list(df['grp_desc'][:-1]) # 获取切割点
bin_desc = getBinDesc(bin_cut) # 获取分箱说明
return bin_cut,bin_desc
# --------卡方分箱的使用Demo-------------------
# ------加载数据-------
iris = load_iris()
x = iris.data[:,0]
y = iris.target
# ----进行卡方分箱------
bin_cut,bin_desc = Chi2Merge(x,y,bin_num=5) # 调用函数进行卡方分箱
bin_stat = statBinNum(x,y,bin_cut) # 统计分箱结果详情
p_list = cal_p(bin_stat.iloc[:,3:]) # 计算相邻分箱间的p值
p_list = [round(p,4) for p in p_list]
# ------打印结果------
print('切割点:' , bin_cut)
print('分箱说明:' , bin_desc)
print('分箱置信度p:', p_list)
print('---------分箱统计----------')
print(bin_stat)
运行结果如下:
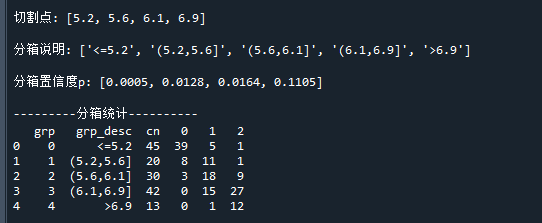
好了,以上就是卡方分箱的原理、流程与及实现代码了~
End
 评论
评论