本站原创文章，转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
DBSCAN聚类全称为Density-Based Spatial Clustering of Applications with Noise，是基于密度的聚类方法
本文讲解DBSCAN聚类的基本思想，以及DBSCAN聚类算法流程，并根据算法流程自写代码实现一个DBSCAN聚类
通过本文可以快速了解DBSCAN的聚类机制和算法流程，以及如何不调函数自行编写代码实现DBSCAN聚类算法
本节介绍什么是DBSCAN聚类，以及一些相关术语
DBSCAN聚类算法介绍
通俗来说，DBSCAN就是从一个样本出发，依靠近邻找近邻，不断把附近的点纳入同一类别
由于DBSCAN是依靠近邻扫描进行聚类，因此DBSCAN的不受样本的形状约束，且具有极强的抗噪性
为了更专业地描述DBSCAN聚类，下面先介绍一些定义
DBSCAN有两个参数：半径 和 最小样本数，以及下述样本类型和关系：
一、样本点的类型
核心样本点：如果样本的半径内的样本个数最小样本数，则称为核心点
核心样本点代表密度足够，核心样本点允许扩散，继续搜索它的近邻点
边界样本点：不是核心样本点，但在其它核心样本点的半径内
边界样本点可以被核心样本点搜索到，但不会进一步搜索它的近邻点
噪声样本点：既不是核心样本点，又不在其它核心样本点的半径内
噪声点不会被核心样本点搜索到，是较为孤立的点
二、样本点的关系
密度直达 ：p是核心点，q在p的范围内，则称p到q是密度直达的
密度直达代表可以通过p直接找到q
密度可达 ：如果p到q可通过一连串的密度直达连接，则称p到q是密度可达的
密度可达代表可以通过p可以找到q
密度相连 ：如果o到p,q都是密度可达的，则称p,q密度相连
密度相连代表p,q能同时被某个点o找到
根据以上定义，DBSCAN的聚类描述如下：
DBSCAN聚类从一个样本点p出发(p必须是核心点，边界、噪声点根本出发不了)
通过密度直达不断传播，直到边界点样本点为止，本次找到的所有样本归为一个类别
可知，所有与p密度可达的样本都会被找到，样本之间的允许的最大跨度是"密度相连"
本节介绍DBSCAN的具体聚类流程，以及展示算法流程图
DBSCAN聚类流程
DBSCAN的算法流程如下：
一、初始化所有样本均未被访问过
二、对所有样本点进行历遍：
1. 如果样本已被访问过：
继续下一个样本
2. 如果不是核心样本点：
将样本标为噪声，并标记样本已被访问，继续下一个样本
3. 如果是核心样本点：
创建一个类别
标记该样本已被访问
将样本的密度直达样本放到搜索队列
历遍搜索队列样本 :
样本还没有类别，则标上当前类别
如果样本被访问过，继续下一个样本
标记样本被访问
如果是核心点，将样本的密度直达样本放到搜索队列，并去重
（备注：后期会有许多样本已被访问，因此在放上队列前可先作筛选）
三、输出最终每个样本的分类
DBSCAN聚类流程图
DBSCAN聚类的算法流程图如下：
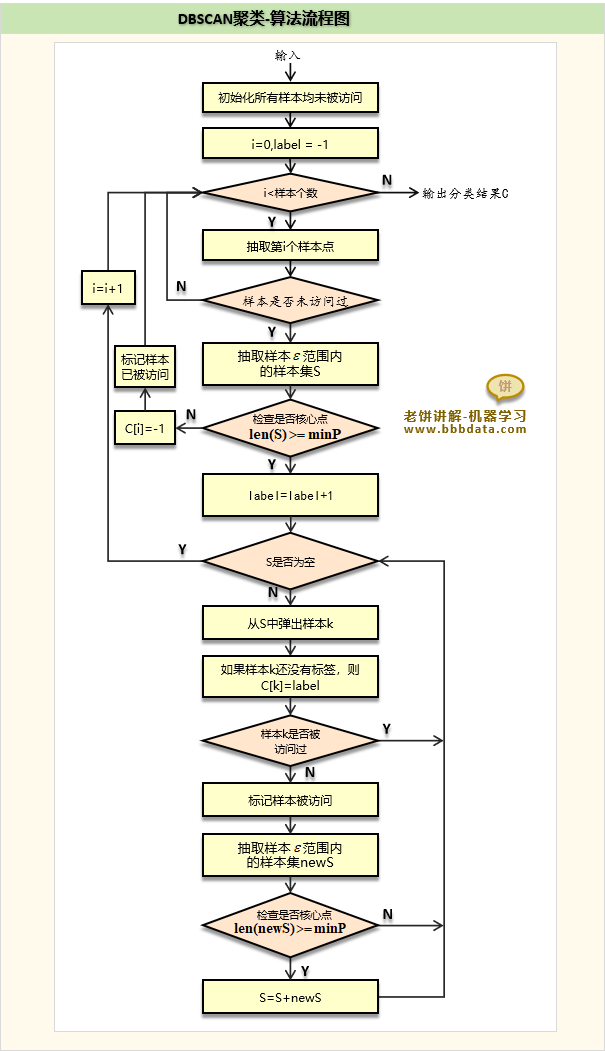
本节展示如何使用代码自行实现DBSCAN聚类算法
自写代码实现-DBSCAN聚类
下面不用软件包，自行实现DBSCAN算法进行聚类
说明：本代码由笔者根据原理的理解编写，仅供参考与学习
具体代码如下：
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# -------------成生数据
X1, y1=datasets.make_circles(n_samples=5000, factor=.5,noise=.05)
X2, y2 = datasets.make_blobs(n_samples=100
,n_features=2
,centers=[[2,2]]
,cluster_std=[[.1]]
,random_state=0)
X = np.concatenate((X1, X2)) # 样本数据
esp = 0.15 # 设置范围
minP= 2 # 最小样本数
n_sample = X.shape[0] # 样本个数
C = np.zeros([n_sample,1]) # 初始化类别
v = np.zeros([n_sample,1]) # 初始化访问表
lable = -1 # 初始化当前类别标签
for i in range(n_sample): # 逐样本循环
if (v[i]==1): # 如果样本已经访问过,则放弃
continue # 直接进入下一次循环
v[i] = 1 # 标记样本已被访问
d = np.sqrt(((X[i]-X)*(X[i]-X)).sum(axis=1)) # 计算距离
d[i] += esp +1 # 为了屏蔽当前样本,将距离置为比eps大
if sum(d<esp)<minP: # 如果不是核心点
C[i] = -1 # 标为噪声样本
continue # 继续下一个样本
search_list= list(np.where(d<esp)[0]) # 找出直达样本作为搜索列表
lable +=1 # 本次的类别标签
C[i] = lable # 标记当前样本的类别
while(len(search_list)>0): # 如果搜索列表不为空,则进行搜索
print(sum(v))
cur_idx = search_list.pop(0) # 从列表中弹出一个样本
cur_x = X[cur_idx] # 获取样本数据
if(C[cur_idx]<=0): # 如果样本还没有类别
C[cur_idx] = lable # 则标示为本类别
if(v[cur_idx]==0): # 如果样本还没被访问过
v[cur_idx] = 1 # 标记样本已经被访问
d = np.sqrt(((X[cur_idx]-X)*(X[cur_idx]-X)).sum(axis=1)) # 计算样本与其它样本的距离
d[i] += esp+1 # 为了屏蔽当前样本,将距离置为比eps大
if sum(d<esp)>=minP: # 如果是核心点
new_p = np.where(d<esp)[0] # 找出当前样本的直达样本
noise_idx = np.where((v[new_p]==1)&(C[new_p]<=0))[0] # 直达样本中之前被认为是噪声的样本
C[noise_idx] = lable # 将其标记本次类别
valid_idx = np.where((v[new_p]==0))[0] # 直达样本中未被访问过的样本
new_search =list(new_p[valid_idx]) # 将其作为新增的搜索样本
search_list= list(set(search_list + new_search)) # 添加到搜索列表
plt.scatter(X[:, 0], X[:, 1], c=C) # 绘制聚类结果
plt.show() # 显示运行结果如下：
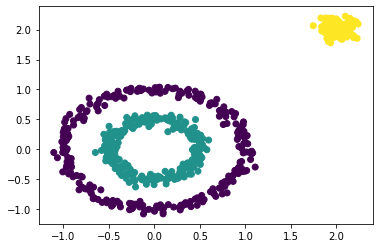
可以看到，自写的算法已经成功地把样本分为三类，说明算法是有效的
End