
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
蒙特卡罗算法是一个强大的算法,本文讲解如何使用蒙特卡罗算法来解决类别识别问题
通过本文,可以进一步加强对蒙特卡罗算法的理解和实际应用
本节介绍螃蟹识别的问题与数据说明
螃蟹类别识别问题介绍
螃蟹类别数据如下:
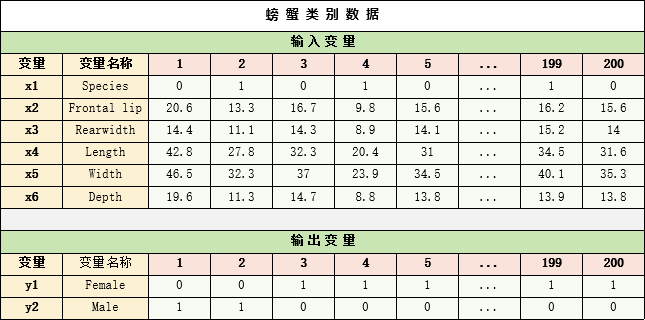
螃蟹类别的输入变量共六个,分别是种类、额唇、后宽度、长度、宽度、深度,
输出为雌、雄两种类别
现需要用采集到的关于螃蟹的六个输入变量来识别螃蟹的性别
本节讲解如何设计一个蒙特卡罗算法来识别螃蟹类别
蒙特卡罗法用于螃蟹识别的算法设计
蒙特卡罗法用于螃蟹识别的算法设计
算法设计如下:
将历史样本存储起来作为一个样本库,
当来了一个新样本时,就在样本库各个类别各抽取n个样本
然后判别新样本中与抽出的样本哪个最相似,就判为哪一个类别
如此重复抽取t次,
最后统计t次中,被判为哪个类别的次数最多,就认为样本属于哪个类别
✍️备注:这里我们使用欧氏距离作为相似度的度量,欧氏距离越小,就认为越相似
蒙特卡罗法用于螃蟹识别的算法流程图
算法流程如下:
本节通过代码实现蒙特卡罗法识别螃蟹类别,并展示相关结果
蒙特卡罗法用于螃蟹识别-代码实现
依据上述算法设计,编码蒙特卡罗法用于螃蟹识别的代码如下:
%------代码说明:展示蒙特卡罗法求解用于螃蟹类别预测 -----------------
% 来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2018a
clc;clear all ;close all ;
rng(999) % 设置随机种子
% 加载数据
load crab_dataset.mat % 加载螃蟹数据
x = crabInputs; % 螃蟹数据的输入变量
y = crabTargets; % 螃蟹的类别数据
x = (x - min(x,[],2))./(max(x,[],2) - min(x,[],2)); % 对x进行归一化
% 将样本分割为样本库样本和测试样本
test_num = 30; % 测试的样本个数
sample_num = size(x,2) - test_num; % 作为样本库的样本个数
rnd_idx = randperm(test_num+sample_num); % 生成随机索引
sample_idx = rnd_idx(1:sample_num); % 样本库的索引
test_idx = rnd_idx(sample_num+1:sample_num+test_num); % 测试样本的索引
sample_x = x(:,sample_idx); % 样本库的输入数据
sample_y = y(:,sample_idx); % 样本库的输出数据
test_x = x(:,test_idx); % 测试样本的输入数据
test_y = y(:,test_idx); % 测试样本的输出数据
% 调用蒙特卡罗法对测试样本进行预测
class_num = size(sample_y,1); % 类别个数
py = zeros(class_num,test_num); % 初始化预测结果
for i = 1:test_num % 逐个样本进行预测
py(:,i) = mc_predict(sample_x,sample_y,test_x(:,i)); % 调用蒙特卡罗法进行样本预测
end
% 统计与打印预测准确率
y_label = vec2ind(test_y); % 将测试数据的真实结果由one-hot格式转为类别标签形式
py_label = vec2ind(py); % 将预测结果的one-hot格式转为类别标签
acc_rate = sum(py_label==y_label)/length(y_label); % 计算准确率
disp(['预测准确率:',num2str(acc_rate)]) % 打印准确率
plotconfusion(test_y,py) % 绘制混淆矩阵其中蒙特卡罗法判断样本类别函数mc_predict的代码如下:
function y = mc_predict(sample_x,sample_y,x)
% 用蒙特卡罗法判断样本的类别
t = 200; % 裁决次数
n = 30; % 每个类别抽样数量
[class_num,sample_num] = size(sample_y); % 类别个数与样本个数
class_idx = cell(class_num,1); % 初始化各个类别的样本索引
for i = 1:class_num
class_idx{i} = find(sample_y(i,:)); % 找出属于第i个类别的样本索引
end
% 进行抽样裁决x的类别
rs = zeros(class_num,t); % 初始化裁决结果表
for i = 1:t
select_idx = zeros(n*class_num,1); % 本次抽样的样本索引
for j = 1:class_num % 逐类别抽样
cur_class_idx = class_idx{j}; % 属于第i个类别的样本索引
cur_select_idx = randperm(length(cur_class_idx),n); % 随机抽出n个样本
select_idx((j-1)*n+1:j*n) =cur_select_idx; % 记录本次抽出的样本索引
end
select_sample = sample_x(:,select_idx); % 抽取出本次抽样的样本
d = sum((select_sample-x).^2); % 计算各个样本与x的距离
[~,win_idx] = min(d); % 找出最小距离的样本作为本次胜出的样本
win_y = sample_y(:,select_idx(win_idx)); % 根据样本的索引找出y
rs(:,i) = win_y; % 记录本次的获胜的y
end
% 统计多次抽样裁决的结果,用于决定最终x的所属类别
win_stat = sum(rs,2); % 统计各个类别胜出的次数
[~,win_idx] = max(win_stat); % 找出哪个类别胜出次数最多
y = zeros(class_num,1); % 初始化x的类别y
y(win_idx) = 1; % 将胜出次数最多的类别,作为x的类别
end运行结果
运行结果如下:
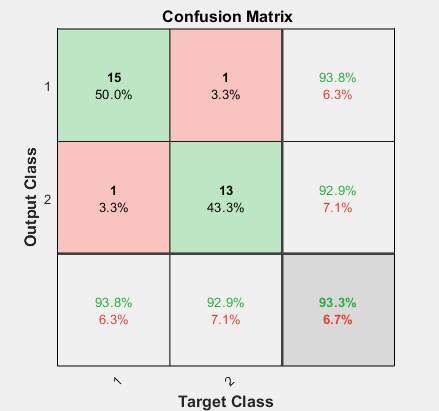
可知,预测准确率达到了93.33%,已经取得了一定的预测效果
End
 评论
评论