
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
自适应梯度下降法是梯度下降法的改进它在梯度下降法的基础上加入了自适应学习率
本文介绍自适应梯度下降法的算法思想和算法流程,并展示自适应梯度下降法的具体实现代码
通过本文,可以快速了解什么是自适应梯度下降法,以及如何使用自适应梯度下降法来解决优化问题
本节介绍自适应梯度下降法的思想与具体算法流程
自适应梯度下降法简介
自适应梯度下降法是什么
自适应梯度下降法是梯度下降法的改进,它加入了自适就学习率的机制,使训练速度加快
自动调整学习率的机制简单来说如下:
1. 如果当前学习率可以让目标函数下降,那么就增大学习率,让它迭代步长更大
2. 如果当前学习率不能让目标函数下降,那么就减小学习率,让它迭代步长变小
自适应梯度下降算法流程
自适应梯度下降算法流程基本与梯度下降法一致,
只是加入了学习率的自适应调整
具体算法流程如下
一、初始化
1. 初始化:
2. 初始化学习率:
3. 初始化学习率上升比:
4. 初始化学习率下降比:
5. 初始化误差最大上升比:
二、迭代
1. 计算F(X)在X处的梯度dX
2. 将X往负梯度方向调整
3. 如果函数值没有上升过多:
接受新解:
4. 调整学习率
(1) 如果函数值得到下降:
增加学习率 :
(2) 如果函数值上升过多:
降低学习率 :
5. 判断终止条件,如果满足终止条件就终止训练
终止训练条件如下
(1) 梯度过小
(2) 函数已达到目标值
(3) 达到最大迭代次数
三、输出训练好的X
自适应梯度下降法算法流程图
自适应梯度下降法的算法流程图如下:
本节利用python进行代码编程,展现如何用代码实现自适应梯度下降算法
自适应梯度下降法-代码实现
下面使用自适应梯度下降算法来求函数的最小值
其中,目标函数的梯度,如下:
,
自适应梯度下降法具体实现代码如下:
"""
自适应梯度下降求y= (x1-2)^2+(x2-3)^2的最小解
"""
import numpy as np
lr = 0.1 # 设置学习率
lr_inc = 1.05; # 设置学习率升上率
lr_dec = 0.7; # 设置学习率下降率
max_inc = 1.04; # 设置减少学习率的阈值
f = lambda x:(x[0]-2)**2+(x[1]-3)**2 # 定义目标函数
x = np.array([0,0]) # 初始化x
y = f(x) # 初始化y
for i in range(100): # 最大迭代100次
dx = np.array([2*x[0]-4, 2*x[1]-6]) # 计算x的梯度
new_x = x - lr*dx # 往负梯度方向更新x
new_y = f(new_x) # 计算新的函数值
if(new_y<y): # 判断是否增加学习率
lr = lr * lr_inc # 增加学习率
elif((new_y/y)>max_inc ): # 判断是否下降学习率
lr = lr * lr_dec # 下降学习率
if((new_y/y)<=max_inc): # 判断是否接受新解
x = new_x # 接受新解
y = new_y # 更新y
if((min(abs(dx))< 0.001) ):break # 如果梯度过小,则退出迭代
print("第"+str(i+1)+"轮迭代:x=:["+str(x[0])+","+str(x[1])+"],y="+str(y)) 运行结果如下:
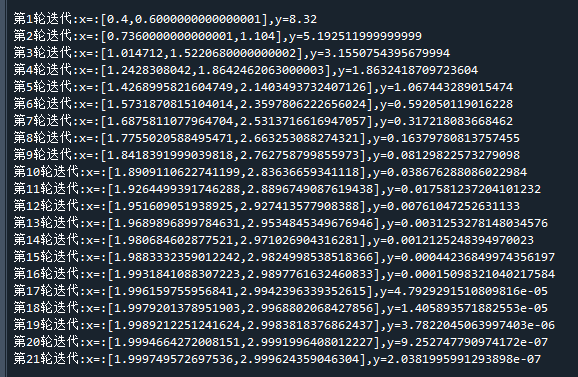
可以看到,经过21轮迭代,求得的 x1,x2= 【1.999,2.999】与真实极值【2,3】已经非常接近了
自适应梯度下降法相比梯度下降算法的速度要快许多,是梯度下降法的一个性价比较高的平替方案
End
 评论
评论