
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
pytroch中自动求梯度看起来很不可思议,但实际并非那么难以理解
本文讲解自动求梯度是如何实现的,并梳理出每一个实现的具体步骤
本节初步讲解自动求梯度的实现思想
01.自动梯度的实现思想
自动求梯度第一次接触时看起来很不可思议,但其实仔细一想,也并非那么玄乎
由于任何一个初等函数,都是多个基本初等函数进行基本运算或者复合而成,
例如可以拆成 两个基本初等函数的复合
因此,只要是初等函数,底层都是最基础的"基本初等函数的求导公式"和"基本求导法则",

只要预先把"基本初等函数的求导公式"和"基本求导法则"实现,
再把初等函数拆成成一个个基本初等函数,根据基本求导法则进行求导就可以了
本节讲解自动求梯度的各个具体步骤,并理解自动求梯度中的运算图概念
01.自动梯度的主要步骤
自动求梯度在具体实现时主要有如下步骤:
👉1. 函数拆解与运算图
把函数拆解成多个基本初等函数,并记录各个基本初等函数之间的关系
它们之间的关系有两种,
(1)复合关系,复合关系的求导顺序为串行关系
(2)基本运算关系,基本运算关系为并行关系
因此,拆解后的各个基本初等函数是串行与并行共存的关系图,
以为例 ,拆解如下:
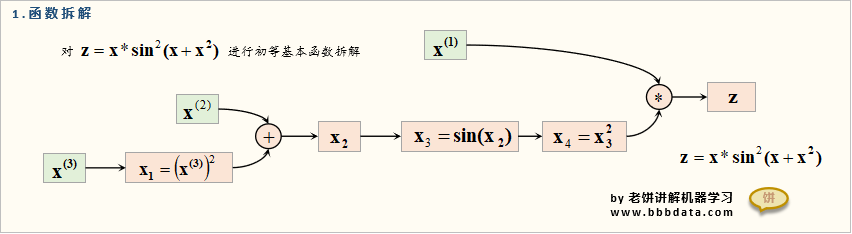
✍️什么是运算图
拆解后得到的这张关系图就称为运算图
👉2.前馈式计算每个节点值
由于求导过程需要用到节点的值,所以预先前馈式算出每个节点的值
👉3.后馈式计算各个节点的梯度
由于复合关系的前后依赖性,因此由后往前对每个节点进行求导,如下:
可以注意到,由于拆解的充分性,在求导过程只涉及基本初等函数的求导公式和基本求导法,
因此只需要预先存储好基本初等函数的求导公式和基本求导法就可以
👉4.累计所有叶子节点梯度
累加所有关于自变量的叶子节点的梯度值,就是自变量的梯度
好了,以上就是实现自动计算梯度的原理了~
End
 评论
评论