
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
BN批归一化是深度学习中的一种归一化方法,它通过解决内部协变量偏移问题来加速网络训练的速度
本文讲解BN批归一化层的原理、BN批归一化层的计算公式,以及批归一化BN的具体代码实现
通过本文,可以快速了解什么是BN批归一化是什么,如何计算,以及在代码中如何应用批归一化层
本节介绍批归一化层是什么,用来干什么,以及BN的计算公式
什么是批归一化BN
批归一化BN(Batch Normalization)是深度学习中的一种归一化方法,用于抑制内部协变量偏移问题
BN批归一化一般用在激活函数之前,通过批归一化可加速模型的训练,是卷积神经网络中常用的一种归一化方法
BN出自Inception-V2原文: 《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》
批归一化顾名思义,是将一批输入进行归一化
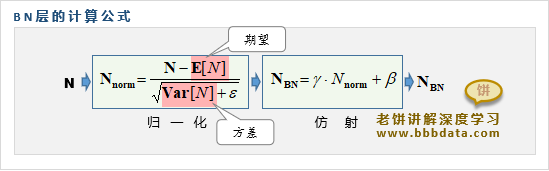
不妨设需要进行归一化的一批输入记为N,则批归一化的计算公式如下:
BN由归一化与仿射两部分组成,它先将输入进行归一化,再用仿射变换还原
各个参数意义如下:
:输入N的期望值,
:输入N的方差,
ε :一个较小的常数,在分母中加入是为了防止分母过小
:待优化的参数,跟着模型一起训练
为什么需要进行批归一化
批归一化BN主要是为了解决训练时内部协变量偏移导致训练较慢的问题,具体如下
内部协变量偏移是什么
在多层神经网络中,由于前层的权重发生变化会导致后一层的输入发生变化
当神经网络层数很多时,前层的变化会经过层层传播,不断扩大,引起后层的极大变化
因此调整前层的权重时,很容易令后层的输入发生极大的变化,这称为内部协变量偏移
内部协变量偏移会导致后层的神经元出现饱和等各种问题,并给训练造成困难
BN是如何消除内部协变量偏移的
BN批归一化的原理就是通过keep住输入的分布来消除内部协变量偏移,从而加速训练
因此,BN批归一化一般嵌入到在神经元值之后、激活函数之前的位置
它先将神经元值进行归一化,再进行仿射变换来还原,从而使得激活前的值的分布稳定,减轻内部协变量偏移带来的影响
本节讲解BN应用于全连接层和卷积层时的归一化方式
BN应用于全连接层与卷积层
BN批归一化应用于全连接层
BN批归一化应用于全连接层时,它将每个神经元值各自进行归一化,如下:
即每个神经元分别独立进行批归一化,此时每个神经元的都是独立的
BN批归一化应用于卷积层
当BN批归一化应用于卷积层时,一般将每个通道各自独立进行批归一化,如下:
即每个通道的都是独立的,其中,单个通道的期望与方差用其所有神经元进行估算
例如一个通道的featureMap为h×w, 共有n个样本, 则用这n×h×w个神经元来估算
卷积之所以按通道进行批归一化,主要是考虑到卷积层单个通道内的各个神经元与周边神经元是相关联的
在归一化时需要保持这个特征,因此,对单通道的神经元应使用统一的参数来进行归一化
BN中的期望与方差的估算方法
在BN层的归一化计算部分,涉及到神经元值N的期望与方差的估算:
在训练阶段与使用阶段分别采取不同的方法估算和
具体如下:
1. 训练阶段
在训练阶段,归一化使用当前批训练数据的期望与方差
2. 模型应用阶段
在模型应用时,可以使用所有训练数据的期望与方差
也可采用抽取最后K次批训练数据的期望与方差进行估算
分别是第i次批训练时的期望和方差
即,训练过程的期望、方差是动态的,它是"当前批"的数据评估期望和方差
而训练完后,用于评估时,则是一个永久的、固定的模型固定的
、 其中,永久的、固定的是由每一批数据的期望和方差动态更新而得到
在pytorch中,model.train()状态时,则代表按输入数据来评估, model.eval()时,则使用固定的
本节展示批归一化的具体代码使用示例
批归一化BN-代码实现
全连接神经网络是按单个神经元进行归一化,它是一维的,而卷积层是按通道进行归一化,它是二维的
因此,在pytorch中,全连接层的批归一化使用BatchNorm1d来实现,而卷积层则使用BatchNorm2d
以卷积层的批归一化为例,代码示例如下:
import torch.nn as nn
import torch
model = nn.Sequential(
nn.Conv2d(1,3, kernel_size=3,padding=2), # 卷积层
nn.BatchNorm2d(3), # 批归一化(共3个通道)
nn.ReLU(inplace=True), # 激活函数
)
model.eval() # 将模型切换为评估状态
x = torch.tensor([[[[0., 1., 2.],[2.,3.,4.],[4.,5.,6.]]]]) # 生成一个tensor数据x
y = model(x) # 计算模型输出如代码所示,在卷积神经网络中,一般在卷积之后使用批归一化,只需在卷积层之后加入批归一化层即可
由于批归一化应用于卷积层时,是按通道进行批归一化的,因此nn.BatchNorm2d(3)中的3就是代表通道数
需要特别说明的是,训练完后需要将模型切换回评估状态,即model.eval(),这样模型的BN层才是用固定的期望、方差
好了,BN层的相关计算公式与代码实现就介绍到这里了~
End
 评论
评论