
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
在pytorch中训练一个模型,往往是直接使用pytorch的优化器对模型进行训练
本文简单介绍pytorch的优化器是什么,并展示如何使用pytorch的优化器对模型进行训练
本节简单介绍pytorch的优化器,并讲述如何使用优化器
什么是pytorch的优化器
在pytorch中训练一个模型,往往是直接使用pytorch的优化器进行训练
优化器指的是pytorch已经写好的一套训练算法
例如常见的SGD(随机梯度下降算法)、LBFGS(拟牛顿法)、Adam等等
对于简单的梯度下降算法,自己手写与调用pytorch的优化器差别不大,
但对于复杂的算法,调用优化器就会方便很多
如何使用pytorch的优化器
使用pytorch的优化器主要包括三个步骤
👉1. 初始化优化器
👉2. 自行更新梯度
👉3. 调用优化器进行参数更新
下面详细介绍使用pytorch优化器时的这三个步骤
优化器的初始化
优化器初始化主要是指出要把哪些参数交给优化器进行优化,及设定优化算法中的超参数
以随机梯度下降SGD为例,初始化一个SGD优化器示例如下:
optimizer = torch.optim.SGD({w,b}, lr=0.01)
其中w和b是我们要优化的参数,而lr则是SGD的超参数-学习率
自行更新梯度
由于优化器更新参数时需要用到参数的梯度,所以需要先自行更新梯度
需要注意的是,pytorch的梯度更新是累加的,因此更新梯度前需要先将梯度清零
为了更方便梯度清零,优化器提供了一次性清零所有参数梯度的方法,如下:
optimizer.zero_grad()
通过zero_grad就会一次性把之前交给优化器管理的参数w和b的梯度都清零
调用优化器进行参数更新
优化器把算法的更新机制进行封装,直接调用就能按算法的机制对参数进行更新
如下,调用下述语句就会利用参数的梯度对参数进行更新
optimizer.step()
以梯度下降为例,optimizer.step()就相当于执行w=w-lr*dw这样的操作
✍️pytorch优化器的使用-总结
根据上述三大步骤的理解,使用优化器优化参数的形式如下:
初始化优化器
for 循环
----清空梯度
----更新梯度
----优化器更新参数
本节展示一个用pytorch的优化器训练一个逻辑回归模型的例子
使用pytorch的优化器训练一个逻辑回归
下面展示如何使用pytorch的优化器训练一个逻辑回归模型
主要就是把《》一文中的训练部分改为使用pytorch的优化器进行参数训练
具体代码如下:
import torch
import matplotlib.pyplot as plt
import numpy as np
# ------训练数据----------------
X = np.array([[2.5, 1.3, 6.2, 1.3, 5.4, 6 ,4.3, 8.2]
,[-1.2,2.5,3.6,4,3.4,2.3,7.2,3.9]]).T # 样本的输入数据
Y = [0,0,1,0,1,1,1,1] # 样本的标签
x = torch.tensor(X) # 将训练数据X转为tensor
y = torch.tensor(Y) # 将训练数据y转为tensor
#-----------训练模型------------------------
w = torch.tensor([2,2],dtype=(float),requires_grad=True) # 初始化模型系数w
b = torch.tensor([1],dtype=(float),requires_grad=True) # 初始化模型系数b
optimizer = torch.optim.SGD({w,b}, lr=0.01) # 初始化优化器
for i in range(1000):
L = (torch.log(1+torch.exp(x@w+b)) -y*(x@w+b)).sum() # 损失函数
print('第',str(i),'轮的Loss:',L) # 打印当前损失函数值
optimizer.zero_grad() # 更新梯度之前先清空梯度
L.backward() # 用损失函数更新模型系数的梯度
optimizer.step()
# --------------------画出结果----------------
print('--------最终结果-------')
W = w.detach().numpy() # 模型的系数,先转回numpy
B = b.item() # 模型的阈值,先转回数值
print('W:',W) # 打印模型系数W
print('B:',B) # 打印模型系数B
x1 = X[:,0] # 绘制分割平面的x轴
x2 = (-B - W[0]*x1)/W[1] # 绘制分割平面的y轴
plt.scatter(X[:, 0], X[:, 1],c=Y) # 绘制样本
plt.plot(x1,x2) # 绘制分割平面
plt.axis([min(X[:,0])-1,max(X[:,0])+1,min(X[:,1])-1,max(X[:,1])+1]) # 设置坐标范围
plt.show() # 展示图象运行结果
运行结果如下:
第 0 轮的Loss: tensor(23.8272, dtype=torch.float64, grad_fn=<SumBackward0>)
第 1 轮的Loss: tensor(23.2013, dtype=torch.float64, grad_fn=<SumBackward0>)
第 2 轮的Loss: tensor(22.5759, dtype=torch.float64, grad_fn=<SumBackward0>)
.....
第 997 轮的Loss: tensor(0.4918, dtype=torch.float64, grad_fn=<SumBackward0>)
第 998 轮的Loss: tensor(0.4913, dtype=torch.float64, grad_fn=<SumBackward0>)
第 999 轮的Loss: tensor(0.4908, dtype=torch.float64, grad_fn=<SumBackward0>)
--------最终结果-------
W: [1.50026373 1.46529551]
B: 0.7041382734007223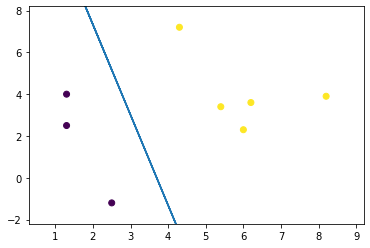
可以看到,逻辑回归模型已成功把样本分为两类,说明训练是成功的
End
 评论
评论