
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
卡方检验一般是指卡方独立检验,它用于检验两组别的分布有没有显著区别
本文讲解卡方检验的原理、计算流程,并通过一个具体例子展示 卡方独立检验的每一个步骤
通过本文,可以快速了解什么是卡方检验,它如何计算,以及如何使用代码实现卡方独立检验
本文讲解卡方检验中的独立检验是什么,以及它的思想原理
卡方独立检验
卡方检验包括独立检验和拟合性检验,它们基于卡方值解决不同的问题
卡方拟合性检验可参考文章《卡方检验-拟合性检验》,本文只讲解卡方独立检验
什么是卡方独立检验
卡方-独立检验解决的问题如下:
事件发生有n种可能 ,A组 和 B组在 上的分布现在表现出来的分别是
、
我们想知道A组与B组在取值分布上有没有区别
卡方独立检验的思想与流程
卡方-独立检验的思路与流程如下:
一、假设没区别,算出期望值
卡方检验先假设A组与B组没有区别,在这假设下,算出A组与B组的期望值
二、计算期望值与事实值差异的概率
计算事实值与期望值的差异(该差异构造成服从卡方分布)
由于差异值服从卡方分布,故可进一步计算出差异值出现的概率
三、根据概率,确定假设成不成立
根据差异值出现的概率,从而确定假设合不合理
如果概率很小,说明当前是个小概率事件,则假设不合理,即A组与B组没有区别
本节讲解卡方独立检验的详细计算流程,以及解释其中涉及的公式
卡方独立检验-计算步骤
事实表是指各组当前观察到的取值,它的格式如下:
一般将事实表记为A,现在要判断A中的组1与组2有没有区别
卡方独立检验的步骤如下:
一、计算期望表
期望表 E 的计算公式为:
其中,为A第i行求和,为A第j列求和,为总样本数
二、计算卡方值
卡方值计算公式为:
三、计算p值
p值如下计算:
其中, :自由度,, r为A的行数,c为A列数
:自由度df的卡方累积分布函数
备注:卡方累积分布函数一般由计算机或查表得到,没有显式公式
卡方独立检验-公式说明
卡方独立检验-期望表的计算公式推导
在卡方独立检验中,涉及期望表的计算,下面对它的计算公式进行推导
设事实表A与它的汇总数据如下所示:
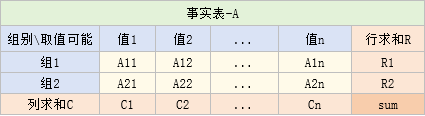
其中,是第i行求和,是第j列求和,是总和
如果组1、组2没有区别,则它们的分布的期望应与总体保持一致
即组1、组2在各个取值上的分布占比都应该为:
由于组1的总样本数为,故组1的期望取值为:
同理,组2的总样本数为,组2的期望取值为:
通过观察就可以得到,期望表的取值为:
卡方独立检验-卡方值与p值的公式解说
由于每一个事实值都与期望值有所差异
不妨用 来量化这个差异,则总的差异为:
设 是服从正态分布的随机变量,则由统计学知识可知:
是服从标准正态分布的随机变量
从而服从自由度为的卡方分布
因此,差异的概率为:
其中, 是自由度为的卡分累积分布函数
即可得到在"组1、组2没区别"的假设下,样本出现当前差异的概率
如果概率过小,则拒绝假设,认为组1、组2存在区别,即p越小,代表两组别的分布区别越大
这里从使用一个实例,感受卡方独立检验是个什么东西,怎么检验的
卡方独立检验-计算实例解说
男女两组身高分布如下:
现问性别对身高有没有影响
卡方独立检验的计算过程如下:
一、 计算期望表
1. 在计算期望表前,先对事实表进行行列汇总,如下:
2. 使用公式 计算期望表, 可得到结果:
即:
二、计算卡方值
根据公式计算卡方值,如下:
卡方值是事实与期望差异的度量
三、计算p值
1. 计算自由度
根据公式计算自由度
2. 计算p值
由 服从自由度为 2 的卡方分布,即可知
其中, 是自由度为2的卡方累积分布函数
使用 python的scipy.stats.chi2.cdf进行计算卡方值
现 , 自由度 , 则代码如下:
即可得到:p = 0.17728440996987782
本节展示卡方独立检验的代码实现,包括调包与自实现
用scipy计算-卡方独立检验
要实现卡方独立检验,可以直接调用scipy的chi2_contingency函数
具体代码如下:
import numpy as np
import scipy
# 本代码用于展示如何使用scipy来计算卡方独立检验
A = np.array([[8,11,1],[3,18,9]]) # 事实表,包含两个组别在3个类别上的样本数
chi2_value,p_value,free_n,ex = scipy.stats.chi2_contingency(A) # 调用scipy的函数计算卡方值与P值
print('\n卡方值chi2 =',chi2_value,',p =',p_value) # 打印卡方值与P值运行结果如下:
从以上结果可以看到,p值相对较小,
如果置信水平设为0.05,由于p<0.05,所以拒绝假设,认为两个组别存在区别
自实现-卡方独立检验
自写代码实现卡方独立检验也是较简单的,只需按照上文的步骤进行实现就可以了
具体代码如下:
import numpy as np
import scipy
# 自实现卡方独立检验
def cal_chi2(pair):
pair[pair==0] = 1 # 避免为0,将0置1
class_rate = pair.sum(axis=1)/pair.sum().sum() # 两类样本的占比
col_sum = pair.sum(axis=0) # 各组别的样本个数
ex = np.dot(np.array([class_rate]).T,np.array([col_sum])) # 计算期望值
chi2 = (((pair - ex)**2/ex)).sum() # 计算卡方值
df = (pair.shape[0]-1)*(pair.shape[1]-1) # 计算自由度
p = 1-scipy.stats.chi2.cdf(df=df, x=chi2) # 返回卡方值与p值
return chi2,p
# 调用自实现函数计算卡方值与P值
A = np.array([[8,11,1],[3,18,9]]) # 事实表,包含两个组别在3个类别上的样本数
chi2,p = cal_chi2(A) # 调用自实现函数计算卡方值与P值
print('卡方值chi2 =',chi2,',p =',p) # 打印卡方值与P值运行结果如下:

可以看到,自写代码计算的卡方值与scipy的函数计算结果是一致的
好了,以上就是卡方检验中的独立检验的原理的计算方法了~
End
 评论
评论