
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
Doolittle分解是矩阵LU分解的一种,它可以把方阵分解成上下三角矩阵的积
本文介绍Doolittle分解的定义、分解的流程与公式推导,并展示Doolittle分解的具体代码实现
通过本文,可以快速了解Doolittle分解是什么,如何进行Doolittle分解以及它的代码实现
本节介绍LU分解中的Doolittle分解是什么,以及分解方法
LU分解与Doolittle分解
LU分解
LU分解是指将方阵A分解为下三角矩阵L与上三角矩阵U的乘积
即
其中
L是下三角矩阵
U是上三角矩阵
Doolittle分解
Doolittle分解则是LU分解方法中的一种,
它的特点是L的对角元素全为1
即Doolittle分解把A分解如下
其中
,
✍️补充:关于LU分解的类别
LU分解从L、U的特点可以分为三种
👉 Doolittle分解 :L对角元全为1(即单位下三角矩阵)
👉 Crout分解 :U对角元全为1(即单位上三角矩阵)
👉 Cholesky分解 :U是L的转置(要求A必须是正定对称方阵)
Doolittle分解的计算公式
Doolittle分解对L、U的求解是
通过对U逐行、L逐列进行迭代式计算求得
即算出U的第1行,再算L的第1列,
然后算U的第2行,再算L的第2列....
U的计算公式
在已算出U的前(i-1)行,L的(i-1)列时,
U的第i列计算公式如下
特别地,U的第1行元素
L的计算公式
在已算出U的前i行,L的(i-1)列时,
L的第i列计算公式如下
特别地,L的第1列元素
本节介绍上节Doolittle分解方法中的公式是如何推导出来的
Doolittle分解-U的求解公式推导
U第i行的求解,可由下式得到
A的第i行为 L的i行乘以U
表示为连加的形式
这是因为L是下三角矩阵,k>i时为0
独立抽出第i个
这是因为Lii=1
根据上式可得到U第i行的求解公式:
因此,在L的前(i-1)列和U的前(i-1)行已求出,即可根据上式求出U第i行的所有元素
补充:上述推导原理对于U的第一行同样适用
U的求解公式推导
L第i列的求解,可由下式得到
A的第i列为 L乘以U 的i列
表示为连加的形式
U是上三角矩阵,k>i时为0
独立抽出第i项
根据上式可得到L第i列的求解公式:
因此,在L的前(i-1)列和U的前 i 行已求出,即可根据上式求出L第i列的所有元素
补充:上述推导原理对于L的第一列同样适用
本节根据上述原理编写Doolittle矩阵分解的实现代码
python代码实现Doolittle矩阵分解
使用python实现Doolittle分解只需按上述理论步骤进行即可
具体代码实现如下:
"""
代码说明:本代码用于实现-Doolittle矩阵分解(LU分解的一种)
本代码来自《老饼讲解-机器学习》www.bbbdata.com
"""
import numpy as np
# Doolittle矩阵分解函数
def DoolittleDecompose(A):
size = A.shape[0] # 方阵的大小
L = np.identity(size) # 初始化L为单位矩阵
U = np.zeros((size,size)) # 初始化U全为0
U[0,:] = A[0,:].copy() # 计算U的第一行
L[:,0] = A[:,0]/U[0,0] # 计算L的第一列
for i in range(1,size): # 逐行、列计算U和L
U[i,:] = A[i,:] - L[i,:i]@U[:i,:] # 计算U的第i行
L[:,i] = (A[:,i] - L[:,:i]@U[:i,i])/U[i,i] # 计算L的第i列
# 为避免过程中产生的一些微小数值问题,将L上三角元素、U的下三角元素置0
L=np.tril(L) # L只取下三角
U=np.triu(U) # U只取上三角
return L,U
# 测试样例
if __name__ == "__main__":
A = np.array([[1.,2.,5,8],[3.,5.,4,2],[6.,4,3,1],[2.,3,5,5]]).T # 生成需要分解的矩阵A
L,U = DoolittleDecompose(A) # 将A进行Doolittle分解
print('\n-----需要分解的矩阵A-----') # 打印标题
print('A=\n',A) # 打印矩阵A
print('\n--------分解的结果------') # 打印标题
print('L=\n',L) # 打印分解后得到的L
print('\nU=\n',U) # 打印分解后得到的U
print('\n---------结果验证--------') # 打印标题
print('\nL*U=\n',L@U) # 打印验证结果代码运行结果如下:
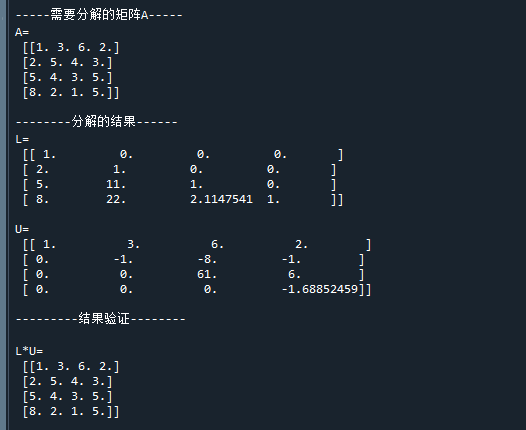
可以看到,Doolittle分解将矩阵A分解为了上三角矩阵L和下三角矩阵U,两者的积就是A
好了,以上就是矩阵LU分解中的Doolittle分解方法与代码实现了~
End