本站原创文章，转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
GBDT全称为Gradient Boosting Decision Tree，是一种用于二分类问题的boosting集成算法
本文介绍GBDT模型、损失函数，以及GBDT的训练算法流程，并展示一个GBDT用于二分类的具体示例
通过本文可以快速了解什么是GBDT集成算法，以及如何实现一个GBDT集成模型来解决二分类问题
本节讲解GBDT集成算法是什么，包括模型的表达式如及损失函数
，
GBDT算法是什么
GBDT梯度提升树，是一种专门用于解决二分类问题的Boosting集成算法
它集成的是回归树，且以样本预测值的损失梯度作为拟合残差，因此称为GBDT梯度提升树
GBDT模型如下：
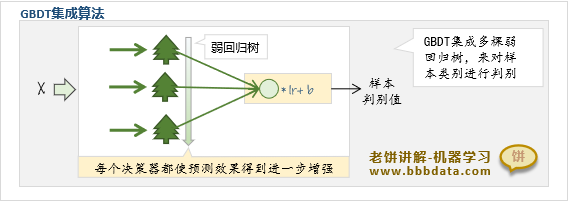
可以看到，GBDT由多棵弱回归树构成，经过学习率lr与阈值b调整后得到样本类别的判别值
一方面它利用了弱回归树的泛化能力，另一方面通过多棵回归树来逐步加强模型的预测精度
GBDT的模型表达式如下
其中，
：第i颗Cart回归决策树的预测值
：学习率，自行设定的超参数
：类别的判别值，g>0时为正样本，g<0时为负样本
从模型的表达式可知，GBDT模型由多个回归树组成
将所有回归树的预测值乘以学习率lr后，加上阈值，就是模型的判别值
✍️GBDT的类别概率
由于GBDT输出的是判别值，如果GBDT模型需要输出概率，则用如下公式：
即在GBDT的判别值上套用sigmoid函数，从而得到样本属于正样本的概率
GBDT的损失函数
GBDT的损失函数采用的是对数似然损失函数
GBDT的损失函数如下：
其中，是第i个样本的真实值
是第i个样本的预测值
本节讲解GBDT模型是如何训练的,以及GBDT的训练流程
GBDT的训练思想
GBDT的训练顺序
GBDT采用前向分步算法训练，就是在已有树模型集合的基础上，再逐个添加新的回归树
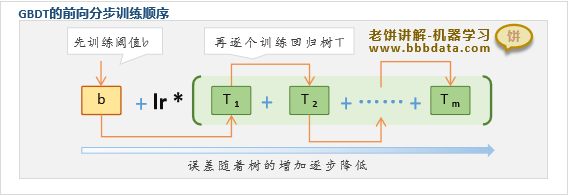
如上图所示，GBDT先训练好阈值b，然后逐棵训练回归树，直到训练完m棵回归树为止
GBDT的回归树训练原理
GBDT采用逐棵树训练的方式，那么每棵回归树是如何训练的呢？
观察到损失函数是关于每个样本预测值的函数，如果往负梯度方向移动， 将下降
基于此思路，GBDT训练新树时，将当前预测值在损失函数的负梯度，作为新树拟合值
可知，GBDT每添加一棵回归树树，所有样本的预测值就往损失函数的负梯度方向挪一下
这就是梯度提升树GBDT，非常形象：每次都往负梯度方向增加树，逐步提升模型的精度
事实上，GBDT“梯度提升决策树”这个命名，就非常形象地解析了GBDT算法的特性：
1、决策树 ：使用一组决策树进行综合决策
2、提升 ：训练时使用提升方式，逐棵逐棵训练
3、梯度 ：每棵树拟合值为树集合预测值的负梯度方向
GBDT的训练流程
GBDT先训练阈值b，再逐棵训练弱回归树T，具体如下：
一、GBDT-阈值b的训练
b的计算公式如下：
说明：该公式由损失函数对b求驻点就可得到
二、GBDT-弱回归树的训练
1. 计算本次回归树每个样本的拟合值(即残差)：
说明：该公式就是损失函数对的负梯度
2. 用上述残差作为每个样本的目标预测值，训练弱回归树
需要注意的是，训练回归树时，要将参数调为训练一棵弱树
例如把最大分裂深度<=3，就是训练弱回归树的一种策略
3. 优化弱回归树的叶子节点
进一步优化本次回归树的预测值，即回归树叶子节点的取值
这样可以使本次新增的回归树能更优地降低GBDT损失函数
回归树中第k个叶子节点的预测值取值如下：
其中,
: 指回归树第k个节点上的所有样本
说明：该公式由损失函数L对叶子节点值求驻点即可得到
总的来说，GBDT就是先训练好阈值b，然后逐棵训练弱回归树
每训练完一棵弱回归树时都优化它叶子节点上的取值，尽可能降低损失函数
GBDT的算法流程
GBDT的训练算法流程如下：
本节展示如何在sklearn中实现一个GBDT模型来对样本进行分类
sklearn实现GBDT的代码示例
下面展示如何构建一个GBDT模型用于类别预测
在sklearn中，只需使用GradientBoostingClassifier函数就可构建一个GBDT模型
GBDT具体实现代码如下：
# -*- coding: utf-8 -*-
"""
本代码展示一个调用sklearn包实现GBDT梯度提升树的Demo
本代码来自《老饼讲解-机器学习》www.bbbdata.com
"""
import matplotlib.pyplot as plt
from sklearn.datasets import make_gaussian_quantiles
from sklearn.ensemble import GradientBoostingClassifier
# --------------- 数据生成 -------------------
# 生成2维正态分布，生成的数据按分位数分为两类，500个样本,2个样本特征，协方差系数为2
X, y = make_gaussian_quantiles(cov=2.0,n_samples=500, n_features=2,n_classes=2, random_state=1) # 生成训练样本数据
#--------------模型训练与预测---------------------
clf = GradientBoostingClassifier(n_estimators=100,learning_rate=0.1,random_state=0) # 初始化GBDT模型
clf.fit(X, y) # 模型训练
pred = clf.predict(X) # 模型预测的类别
proba = clf.predict_proba(X) # 模型预测的概率
# ----------------- 打印结果-------------------------
fig, axes = plt.subplots(2, 1,figsize=(10, 6)) # 初始化画布
plt.subplots_adjust(wspace=0.2, hspace=0.3) # 调整画布子图间隔
axes[0].scatter(X[:, 0], X[:, 1], c=y) # 画出样本与真实类别
axes[0].set_title('sample-true-class') # 设置第一个子图的标题
axes[1].scatter(X[:, 0], X[:, 1], c=pred) # 画出样本与预测类别
axes[1].set_title('sample-predict-class') # 设置第二个子图的标题
plt.show() # 显示画布
print("\n----前10个样本预测结果-----:\n",proba[1:10,1]) # 打印前10个样本的预测值运行结果如下：
从图中可以看到，模型的预测类别与真实类别几乎是一致的
End
