
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
岭回归(Ridge Regression)模型是一种带有正则项的线性模型,它是线性回归的一种改进
本文讲解岭回归模型,包括模型表达式、损失函数、代码实现例子、以及岭迹图的绘画与使用等
通过本文可以快速了解什么是岭回归模型,如何使用岭回归模型,以及怎么看岭迹图
本节介绍岭回归模型的思想、表达式以及损失函数,快速了解岭回归模型是什么
岭回归模型
岭回归模型(Ridge Regression)是线性回归的一种改进,主要是线性回归求得的系数可能会过大
因此,岭回归在线性回归的基础上,在线性回归模型的MSE损失函数中加入二范正则项,以惩罚过大的系数
岭回归的模型表达式与损失函数
岭回归的模型表达式为:
岭回归的损失函数如下:
其中,:样本个数
:系数个数
:y的预测值
:y的真实值
:惩罚系数,用于调节系数W的惩罚力度
当 越大时,惩罚力度越大, 各个系数求出来的绝对值就会越小
✍️饼语:可见,岭回归与线性回归是类似的,仅是损失函数中加入了二范正则项
岭回归的模型求解公式
岭回归的模型求解公式如下:
它与线性回归的求解公式相似,只是部分需要在对角元素上加上
关于岭回归的阈值
可以注意到,岭回归模型是不带阈值的
这是因为岭回归的目的对各个w进行惩罚,而阈值b是不需要惩罚的
虽然岭回归默认不带阈值,但对于线性模型,有阈值与无阈值是可以相互转化的
岭回归拓展阈值b的方法
将岭回归模型拓展成带阈值模型的操作方法如下:
可以先将数据中心点移到原点,以无阈值形式算出W,再通过W算出b.
具体如下:
(1) 先将数据作中心化转换:
此时, 都是以(0,0)为中心的数据
(2) 用训练岭回归模型, 得到
(3) 训练后再计算阈值b:
即可得到
本节展示一个岭回归模型的使用例子以及代码实现
岭回归使用例子
现有数据以下
备注:以上数据的实际关系为:
下面我们建立岭模型,用变量 x1,x2 预测y
用sklearn包求解岭回归模型
用python的sklearn实现岭回归模型,只需调用linear_model.Ridge()函数
岭回归模型Ridge共两个关键参数:
👉alpha : alpha是系数w的惩罚系数,alpha设得越大,模型的参数就越小
👉fit_intercept:岭回归默认是没有阈值的,fit_intercept设为True时,则模型为带阈值模型
sklearn实现岭回归模型代码如下:
from sklearn import linear_model
import numpy as np
#输入数据
x = np.array([[0, 2], [1, 1], [2,3],[3,2],[4,5],[5,2]])
y = np.array([8,7,15,14,25,18])
#调用sklearn的线性模型包,训练数据
ridge = linear_model.Ridge(alpha=1,fit_intercept=True) # 模型实例化
ridge.fit(x,y) # 模型训练
#输出模型系数和阈值
print("当前alpha:"+str(ridge.alpha))
print("模型参数:"+str(ridge.coef_))
print("模型阈值:"+str(ridge.intercept_))运行结果
代码运行结果如下:
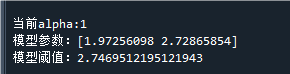
将权重与阈值代入岭回归模型数学表达式,可得
可以看到,它与真实关系 有所偏差,这主要是我们对权重进行了惩罚
本节讲解岭回归的岭迹图,包括如何画岭迹图,怎么看岭迹图
岭迹图是什么
什么是岭迹图
岭迹图指的不同的w随着alpha的取值的变化图,示例如下:
其中横轴是alpha的值,纵轴是各个权重参数的值
从图中可以看到,变量1与变量2的权重参数w1与w2随着alpha增大而减小
绘制岭迹图的代码示例如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
#输入数据
x = np.array([[0, 2], [1, 1], [2,3],[3,2],[4,5],[5,2]])
y = np.array([8,7,15,14,25,18])
#
alpha_list = np.linspace(0,5,20) # 设置要尝试的alpha
w_arr = np.empty((len(alpha_list),x.shape[1])) # 用于记录不同alpha下的权重参数
for i in range(len(alpha_list)): # 逐个alpha训练模型
ridge = linear_model.Ridge(alpha=alpha_list[i],fit_intercept=True) # 模型实例化
ridge.fit(x,y) # 模型训练
w_arr[i] = ridge.coef_ # 记录当前的权重参数
for i in range(w_arr.shape[1]):
plt.scatter(alpha_list, w_arr[:,i], facecolors='none' # 画出每个参数的变化
,edgecolors=np.random.rand(1,1,4),marker='o',label='w'+str(i+1))
plt.legend() # 显示图例 岭迹图怎么看
岭迹图的用途主要有两个:
👉1. 用于确定alpha的取值
👉2.分析变量
如何根据岭迹图确定alpha
根据岭迹图确定alpha,一般紧扣如下两点思想:
(1) w不要过大 :w过大往往不合理,所以所取的alpha要令整体w都不要偏大
(2) alpha尽量小:在保障w不太大的前提下,尽量取更小的alpha
因为alpha过大会使损失函数过于倾向正则项,而忽视了误差项
往往是如下图所示,在喇叭口前取alpha的值:
如何根据岭迹图分析变量
可以借助岭迹图对变量进行分析,但并没有统一、固定的方法,
往往都是较为灵活地进行变量分析,下面仅举例作为思想参考
👉情况一、alpha为0时很w大,在alpha稍微变大时,w迅速趋0
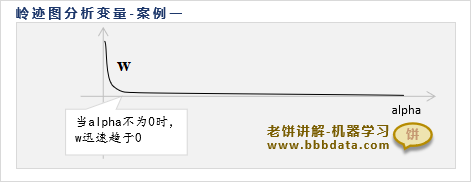
上图中的这种情况,一般可以认为这个变量没有什么用
因为alpha为0时w很大,所以alpha为0时这个变量没什么用
alpha不为0时,w已经趋0,所以变量没有贡献,即这时变量也没什么用
👉情况二、w随着alpha的增大,在正负之间反复跳动
w在正负之间反复跳动,说明变量对y一会是正贡献,一会是负贡献
即变量是非常不稳定的,只要alpha稍微变动一下,正负贡献就相反了
而一个好的、稳定的变量,它对y的贡献应该也是稳定的
岭迹图综合例子讲解
以上述例子中的岭迹图为例,我们综合性地看岭迹图
如果单从本案例的岭迹图来看,alpha设为0就可以了,因为系数在alpha=0时本身就不太大
同时也可以看到两个变量都不会因为alpha的改变而大幅度变动,说明两个变量都比较稳定
好了,以上就是岭回归模型的相关内容了~
End
 评论
评论