
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
SOM全称为自组织竞争神经网络(Self-organizing Feature Map),是Kohonen提出的一种聚类模型
本文介绍SOM神经网络的模型结构、拓扑图以及模型训练方法,并展示一个SOM神经网络的代码实现
通过本文,可以快速了解SOM神经网络是什么、有什么用,以及如何使用SOM神经网络来对样本进行聚类
本节先简单回顾Kohonen规则,并描述性讲述SOM神经网络是什么
SOM神经网络是什么
SOM(自组织竞争)神经网络是一种基于kohonen规则的聚类算法
kohonen规则
kohonen规则进行聚类的方法如下:
先随机初始化k个聚类中心点,然后每次选出一个样本,
将离它最近的聚类点往它移动,使该聚类点更靠近它,如此反复m次
kohonen更新法则如下:
其中
:离样本最近的聚类中心点
: 学习率
kohonen规则虽然简单,然而它却是行之有效的
SOM神经网络
SOM神经网络用于解决聚类问题,它是Kohonen规则聚类的改进
SOM在更新离样本最近的聚类中心P时,会把P的邻近聚类中心也一起更新
更细节的,有以下三点:
1、更新邻近聚类点
更新样本最近点P的同时,P的邻近聚类点也一起更新
(P的学习率要比邻近聚类点更大一些)
2、增加学习率的收缩机制
随着更新步数,学习率越来越小
3、邻近距离收缩机制
随着更新步数,邻近距离阈值越来越小
渐渐的,就只更新目标点及其邻边聚类点
SOM模型在对样本进行判别时,只需要判断样本离哪个聚类中心点近,就判为哪个聚类点
SOM的距离与邻近点
初学者很容易误会,以为SOM训练时所用的邻近聚类点就是目标聚类点附近的聚类点
其实不是,SOM训练时使用的“邻近聚类点”有自己的定义
SOM是先引入一个拓扑结构,把所有聚类点连结在一起,然后籍此来定义距离
拓扑结构与距离
SOM聚类点的拓扑结构可以是一维的,二维的,三维的,或者更高维的
但SOM中最常用是二维的六边形拓扑结构,如下:
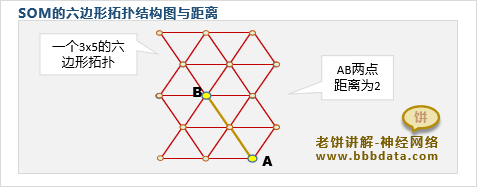
在SOM中,两点的距离,则是指在拓扑结构中,这两点之间的最小边数
SOM的邻近聚类点
SOM每次更新会把邻近聚类点一起更新
对于点P,它的邻近聚类点是指,与P的最小连结边数小于某个阈值的聚类点
例如,当距离阈值设置为2时,则是到达点P不超过2条边的聚类点
所以,SOM中的邻近聚类点并不是用实际距离来区分,而是按拓扑结构中的距离来区分
本节讲解SOM神经网络的数学表达式与拓扑图,进一步具体了解SOM是什么
SOM神经网络的模型表达式
SOM的模型数学表达式为:
其中,dist :欧氏距离函数
compet :竞争函数
简单来说,就是x离哪个聚类中心(即W的每一行)最近,就为1,其余为0
✍️ dist 和compet函数的计算例子
一、dist的计算举例
dist为欧氏距离函数,
例如,2输入、3隐节点时,x和W如下:
,
则:
二、 compet的计算举例
compet 为竞争函数,它将向量最大的值置为1,其余置0
例如,compet([ 2 5 3 ]) = [ 0 1 0 ]
SOM神经网络拓扑图
SOM神经网络是典型的三层神经网络
SOM的网络拓扑图如下,第一层是输入层,第二层是隐层,第三层是输出层
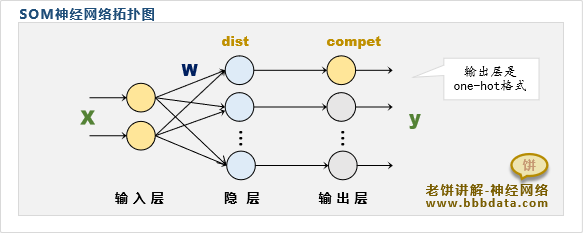
隐节点的意义如下:
1. 隐节点的意义就是聚类中心点
有多少个隐节点就代表有多少个聚类中心点
2. 隐节点的权重W就是聚类中心点的位置
输出层的意义如下:
1. 输出层是one-hot格式(即[0 0 0 1]这样的格式)
2. 输出节点个数与隐层节点个数一致,并与隐节点一一对应
3. 输出节点的值由隐层节点竞争得到
即隐层节点哪个值最大,对应的输出节点就为1,其余为0
✍️带隐层拓扑结构的SOM神经网络拓扑图
往往还会把隐层节点之间的拓扑结构一起画上, 则SOM的网络拓扑图会如下:
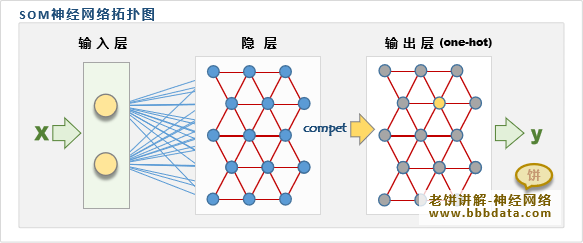
往往我们看到的都是带隐节点拓扑结构的拓扑图,很容易误会,以为隐层节点之间相互连接
其实隐节点的拓扑图只在训练阶段用于获取邻域节点,与最终的模型并没有任何关系的
本节讲解如何实现一个SOM神经网络来对样本进行聚类
SOM神经网络DEMO代码
下面,我们先随机初始化一些样本点,然后调用matlab的神经网络工具箱训练一个SOM神经网络
具体代码如下:
% 本demo展示用matlab工具箱训练一个SOM神经网络
% 生成用于聚类的数据
rand('seed',70); % 随机种子,设定随机种子是为了每次的结果一样
dataC = [2.5,2.5;7.5,2.5;2.5,7.5;7.5,7.5]'; % 生成四个样本中心
sn = 80; % 样本个数
X = rand(2,sn)+dataC(:,mod(1:sn,4)+1); % 随机生成样本点
% 调用工具箱训练一个SOM网络
net = selforgmap([3 5]); % 建立一个SOM神经网络
net = train(net,X); % 训练网络
W = net.IW{1}; % 网络的权重,也即各个聚类中心的位置
y = net(X); % 用训练好的网络进行预测
classes = vec2ind(y); % 将预测结果由one-hot格式转为类别索引
% 绘图
plot(X(1,:),X(2,:),'*'); % 原始样本
hold on
plot(W(:,1),W(:,2),'or','MarkerFaceColor','g'); % 网络训练好的聚类中心运行结果如下:
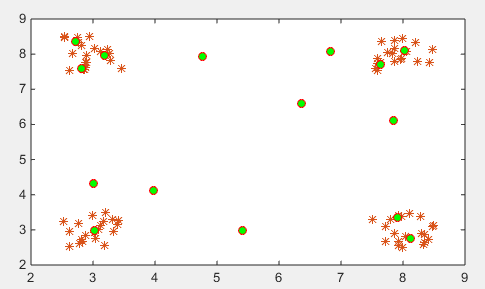
绿色的隐神经元(聚类中心),红色的是样本
End
 评论
评论