
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
LeNet是最早的卷积神经网络之一,由Yann LeCun等人在1998年提出,用于手写数字的识别
本文讲解LeNet卷积神经网络的模型结构,以及每一层的详细计算方法,并展示LeNet-5的代码实现
通过本文,可以快速了解LeNet神经网络是什么,它的具体结构以及计算过程是什么,并掌握LeNet的代码实现
本节对LeNet-5的网络结构进行简单描述,快速了解LeNet-5是什么
LeNet卷积神经网络是什么
LeNet是由Yann LeCun在1998年提出的一种用于解决手写数字的识别问题的CNN卷积神经网络
LeNet原文地址:《Gradient-based learning applied to document recognition》
LeNet-5结构简介
LeNet是一系列模型,但核心模型就是LeNet-5,一般所说LeNet指的就是LeNet-5
在原文中,LeNet-5用于解决手写数字的识别,输入手写数字图片(28×28),输出所属数字类别
LeNet-5原文中提供的网络结构示图如下:
原文的结构图较难理解,不妨看简化后的结构,如下:
如图所示,LeNet一共有7层, 包含3个卷积层(C),2个采样层/池化层(S),和2个全连接层(F)
也可以将它看作[C1,S2]+[C3,S4]+[C5]+F6+F7的结构,这样则是五大层
其中前三大层由卷积和池化组成,用于特征提取,而后两个全连接层则用于拟合输出
本节介绍LeNet-5各层的结构及运算细节
LeNet-5的详细运算流程
LeNet-5的输入:28×28×1的图片(手写数字)
LeNet-5的输入:图片所属类别的判别值向量
一、LeNet-C1层
C1的输入:C1是卷积层,它的输入是28×28×1的图片
C1的运算:C1利用6个5×5×1的卷积核进行卷积,填充为2,步幅为1
卷积后的输出则为6个(28+4-5+1)×(28+4-5+1)=28×28的FeatureMap
C1的输出:28×28×6的特征映射图
二、LeNet-S2层
S2的输入:S2是采样层(池化层),它的输入是C1的输出,即28×28×6的特征映射图
S2的运算:S2的运算包括池化与激活两个步骤
1. 池化:采用Size为2×2,步幅为2的池化窗口对输入进行均值池化
原文这里是采样层,类似于池化,但它是将窗口所有值相加,再乘以一个系数,并加上阈值
原文是希望不同通道用不同系数,使得输出通道有些是高频信息,有些是低频信息
池化后为6个(28/2)×(28/2)=14×14的特征映射图
2. 激活:将池化后的结果使用Sigmoid函数进行激活
S2的输出:14×14×6的特征映射图
三、LeNet-C3层
C3的输入:C3是卷积层,它的输入是S2的输出,即14×14×6的特征映射图
C3与S2的连接方式:C3与S2的连接方式较为特殊,采用非完全连接方式
C3共有16个5×5×1的卷积核,C3与S2的连接方式详细如下:
总的来说,共有四种连接类型
👉1.前6个只连续连接三组
👉2.后6个只连续连接4组
👉3.再之后的3三个只连接不连续的4组
👉4.最后一个是全连接
备注:这样的连接在生物意义上理解为尽量充分地从不同角度、不同粒度地观察S2
C3的运算:C3使用16个5×5×1的卷积核进行卷积,填充为0,步幅为1
卷积后的输出则为16个[(14+4-5)/1+1]×[(14+4-5)/1+1]=10×10的特征映射图
C3的输出:10×10×16的特征映射图
四、LeNet-S4层
S4的输入:S4是采样层(池化层),它的输入是C3的输出,即10×10×16的特征映射图
S4的运算:S4采用Size为2×2,步幅为2的池化窗口对输入进行均值池化
与S2类似,原文这里是采样层,即将窗口所有值相加,再乘以一个系数,并加上阈值
池化后为[10/2]×[10/2]=5×5的特征映射图
S4的输出:5×5×16的特征映射图
五、LeNet-C5层
C5的输入:C5是卷积层,它的输入是S4层的输出,即5×5×16的特征映射图
C5的运算:C5使用120个5×5×16的卷积核进行卷积,填充为0步幅为1
卷积后的输出则为1×1×120的特征映射图
C5的输出:1×1×120的特征映射图
六、LeNet-F6层
F6的输入:F6是全连接层,它的输入是S4层的输出展平后的向量,即120×1向量
F6的运算:F6是传统神经网络的运算方法,激活函数使用tanh
F6的计算具体如下:
其中:
X:120*1的输入向量
W:权重,84×120的矩阵
b:阈值,84×1的列向量
tanh:双曲正切函数
y:F6层的输出
F6的输出:84×1的列向量
七、LeNet-F7层
F7的输入:F7是最后的输出层,它是全连接层,它的输入是F6层的输出,即84×1的列向量
F7的运算:有多少个类别,F7就有多少个神经元,F7与F6全连接,用RBF函数作为激活函数
F7的计算公式如下:
其中,是F7的第i个输出
是F6层第j个神经元与F7第i个神经元的权重
F7的计算示图如下,简单来说,就是F6的输出与W的欧基里得距离:
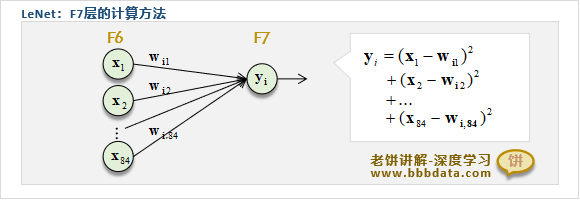
F7的输出:类别个数*1的列向量
F7层的意义如下:
不妨记F6与F7第i个神经元相连的84个权重记为
的意义实际是代表第i个类别的坐标,F6的输出与的距离越近,则输出就越小
最终对比F7的所有输出值,如果第k个输出值最小,就判为第k类
注意,F6与F7的连接权重是根据背景意义精心设计的,设计完后可以在训练中调整,也可以不调整
Lenet-5的运算流程图总览
Lenet-5各层的参数配置如下:
为方便理解,笔者整理出LeNet-5各层的处理流程图,如下:
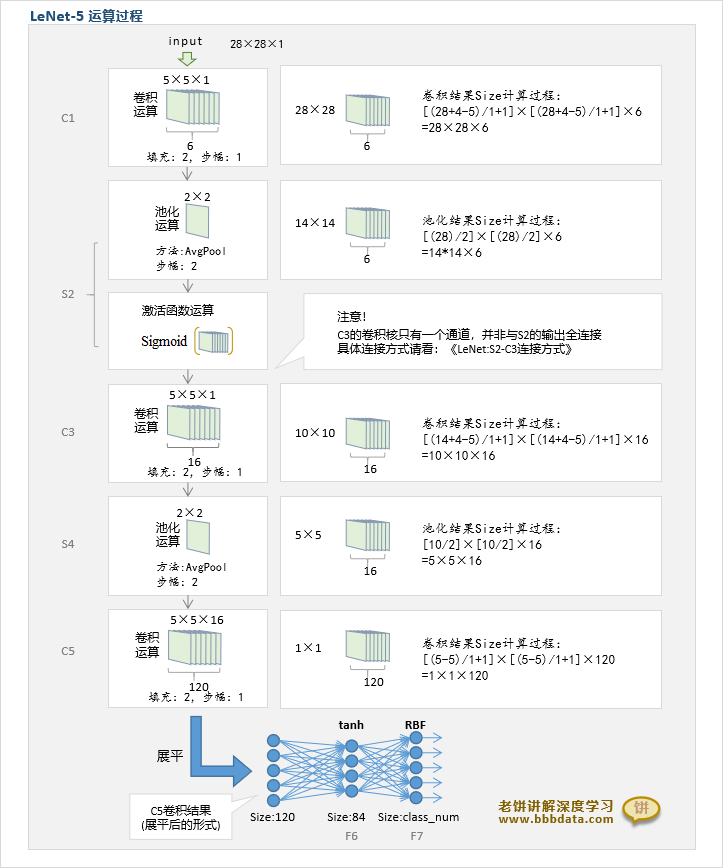
结合上图与第二节的描述进行理解,就可以非常细节与具体地理解LeNet-5的结构与计算方法
本节讲解LeNet-5的具体代码实现
LeNet-5-代码实现
一般很少会再按LeNet-5原文的网络结构去复现LeNet-5,笔者认为有三个原因:
1.F7层使用的是RBF函数,并且F7的权重需要根据具体业务背景精心设计,所以难以复现
2.LeNet-5是一个初代的卷积神经网络,有些细节技术方面在后来并没有太多价值,强行实现也没有太大好处
例如池化层加权重、C3的非完全连接与F7的RBF激活函数等等,都已经被淘汰了,强行实现没有太大价值
总的来说,知道LeNet就好了,初学者不要太纠结一定要按原文去复现,对学习、实际使用都没有太大的价值
下面按现在的流行思想,对LeNet-5的配置略作修改,不完全严谨地实现LeNet
修改后的LeNet配置如下:
LeNet具体代码如下:
import torch
from torch import nn
from torch.utils.data import DataLoader
import torchvision
import numpy as np
#--------------------模型结构--------------------------------------------
# 卷积神经网络的结构
class ConvNet(nn.Module):
def __init__(self,in_channel,num_classes):
super(ConvNet, self).__init__()
self.nn_stack=nn.Sequential(
#--------------C1层-------------------
nn.Conv2d(in_channel,6, kernel_size=5,stride=1,padding=2),
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Sigmoid(),
# 输出14*14
#--------------C2层-------------------
nn.Conv2d(6,16, kernel_size=5,stride=1,padding=0),
nn.AvgPool2d(kernel_size=2,stride=2),
# 输出7*7
#--------------C3层-------------------
nn.Conv2d(16,120,kernel_size=5,stride=1,padding=0),
# 输出1*1*80
#--------------全连接层F4----------
nn.Flatten(), # 对C3的结果进行展平
nn.Linear(120, 84),
nn.Tanh(),
#--------------全连接层F5----------
nn.Linear(84, num_classes)
)
def forward(self, x):
p = self.nn_stack(x)
return p
#-----------------------模型训练---------------------------------------
# 参数初始化函数
def init_param(model):
# 初始化权重阈值
param_list = list(model.named_parameters()) # 将模型的参数提取为列表
for i in range(len(param_list)): # 逐个初始化权重、阈值
is_weight = i%2==0 # 如果i是偶数,就是权重参数,i是奇数就是阈值参数
if is_weight:
torch.nn.init.normal_(param_list[i][1],mean=0,std=0.01) # 对于权重,以N(0,0.01)进行随机初始化
else:
torch.nn.init.constant_(param_list[i][1],val=0) # 阈值初始化为0
# 训练函数
def train(dataloader,valLoader,model,epochs,goal,device):
for epoch in range(epochs):
err_num = 0 # 本次epoch评估错误的样本
eval_num = 0 # 本次epoch已评估的样本
print('-----------当前epoch:',str(epoch),'----------------')
for batch, (imgs, labels) in enumerate(dataloader):
# -----训练模型-----
x, y = imgs.to(device), labels.to(device) # 将数据发送到设备
optimizer.zero_grad() # 将优化器里的参数梯度清空
py = model(x) # 计算模型的预测值
loss = lossFun(py, y) # 计算损失函数值
loss.backward() # 更新参数的梯度
optimizer.step() # 更新参数
# ----计算错误率----
idx = torch.argmax(py,axis=1) # 模型的预测类别
eval_num = eval_num + len(idx) # 更新本次epoch已评估的样本
err_num = err_num +sum(y != idx) # 更新本次epoch评估错误的样本
if(batch%10==0): # 每10批打印一次结果
print('err_rate:',err_num/eval_num) # 打印错误率
# -----------验证数据误差---------------------------
model.eval() # 将模型调整为评估状态
val_acc_rate = calAcc(model,valLoader,device) # 计算验证数据集的准确率
model.train() # 将模型调整回训练状态
print("验证数据的准确率:",val_acc_rate) # 打印准确率
if((err_num/eval_num)<=goal): # 检查退出条件
break
print('训练步数',str(epoch),',最终训练误差',str(err_num/eval_num))
# 计算数据集的准确率
def calAcc(model,dataLoader,device):
py = np.empty(0) # 初始化预测结果
y = np.empty(0) # 初始化真实结果
for batch, (imgs, labels) in enumerate(dataLoader): # 逐批预测
cur_py = model(imgs.to(device)) # 计算网络的输出
cur_py = torch.argmax(cur_py,axis=1) # 将最大者作为预测结果
py = np.hstack((py,cur_py.detach().cpu().numpy())) # 记录本批预测的y
y = np.hstack((y,labels)) # 记录本批真实的y
acc_rate = sum(y==py)/len(y) # 计算测试样本的准确率
return acc_rate
#--------------------------主流程脚本----------------------------------------------
#-------------------加载数据--------------------------------
train_data = torchvision.datasets.MNIST(
root = 'D:\pytorch\data' # 路径,如果路径有,就直接从路径中加载,如果没有,就联网获取
,train = True # 获取训练数据
,transform = torchvision.transforms.ToTensor() # 转换为tensor数据
,download = True # 是否下载,选为True,就下载到root下面
,target_transform= None)
val_data = torchvision.datasets.MNIST(
root = 'D:\pytorch\data' # 路径,如果路径有,就直接从路径中加载,如果没有,就联网获取
,train = False # 获取测试数据
,transform = torchvision.transforms.ToTensor() # 转换为tensor数据
,download = True # 是否下载,选为True,就下载到root下面
,target_transform= None)
#-------------------模型训练--------------------------------
trainLoader = DataLoader(train_data, batch_size=100, shuffle=True) # 将数据装载到DataLoader
valLoader = DataLoader(val_data , batch_size=100) # 将验证数据装载到DataLoader
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 设置训练设备
model = ConvNet(in_channel =1,num_classes=10).to(device) # 初始化模型,并发送到设备
lossFun = torch.nn.CrossEntropyLoss() # 定义损失函数为交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01,momentum =0.9) # 初始化优化器
train(trainLoader,valLoader,model,1000,0.01,device) # 训练模型,训练100步,错误低于1%时停止训练
# -----------模型效果评估---------------------------
model.eval() # 将模型切换到评估状态(屏蔽Dropout)
train_acc_rate = calAcc(model,trainLoader,device) # 计算训练数据集的准确率
print("训练数据的准确率:",train_acc_rate) # 打印准确率
val_acc_rate = calAcc(model,valLoader,device) # 计算验证数据集的准确率
print("验证数据的准确率:",val_acc_rate) # 打印准确率代码运行结果如下:
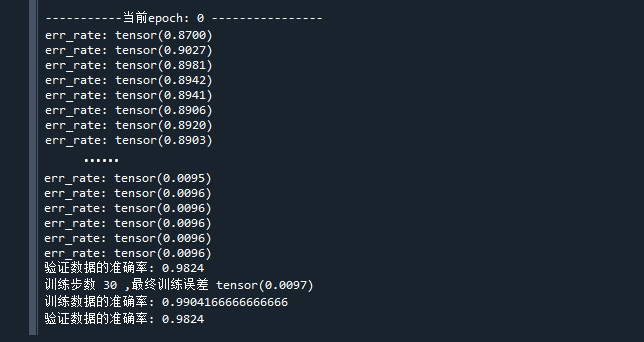
在训练了30个epoch之后,误差下降到0.01,终止训练
可见,LeNet在解决手写字识别上是有效的
End
 评论
评论