
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
SVM(Support Vector Machine)支持向量机是机器学习中知名的、经典的模型之一
本文讲解什么是SVM,包括SVM的思想、模型、以及损失函数,并展示相关的代码例子
通过本文,可以快速知道什么是SVM模型,了解SVM的基本概念以及如何上手使用SVM模型
本节初步了解SVM支持向量机是什么,包括判别面、支持面、支持向量、硬间隔、软间隔等概念
什么是支持向量机
支持向量机SVM主要用于解决二分类问题,即预测样本是正样本还是负样本
SVM的判别面
如上图所示,SVM最原始的目标是找出一个判别超平面,把样本按类别一分为二
能令样本分开的平面非常多,而SVM的目标是令样本离判别平面的最小距离最大化
遗憾的是,最小距离是是无法直接表示出,所以要直接寻找这样的判别面是困难的
SVM的支持面
SVM转换思路,引入了两个支持面来间接找出判别面,如下所示:
支持面是一对平行面,它们之间的距离越大越好,在最大间隔化时它们是两类样本的边界
进一步地,定义两个支持面的中心就是判别面,所以找到支持面,同时也就找到了判别面
软间隔与硬间隔
SVM分为硬间隔模型和软间隔模型,它们分别如下:
SVM硬间隔模型
SVM最早提出的模型是硬间隔模型,它的前提是正负两类样本必须线性可分
硬间隔模型在两个支持面之间没有任何样本的前提下,尽量最大化支持面的间隔
但实际中样本往往是线性不可分的,难以满足硬间隔模型,于是引入了软间隔模型
SVM软间隔模型
实际中常用的SVM模型指的是软间隔模型,软间隔模型不要求样本线性可分
软间隔SVM模型在尽量最大化两个支持面间隔的同时,尽量最小化错误样本个数
最终,软间隔模型在"最大间隔"与"最小错误"两者之间取得一个均衡点作为最优解
本节讲解SVM模型的数学表达式以及损失函数
SVM的模型表示
判别面与支持面的表示
支持向量机的判别面、支持面是三个平行面,因此它们的数学表示为:
支持面:
判别面:
进一步可得,判别面与支持面的距离为:
✍️解说
由于支持面是两个平行面,不失一般性,可以设两个支持面为:
而判别面是两个支持面中间的平行面,因此,判别面的表示就为:
进一步由公式距离可知,判别面与支持面的距离为
注意,由于支持面对称地设为,因此w不仅决定了它们的方向,还决定了它们的距离
SVM的模型表达式-判别函数
在应用SVM模型时,使用的是SVM的判别函数
SVM的判别函数如下表示
当判别值则判为正样本
当判别值则判为负样本
支持面与判别面的距离为d,而判别值 代表样本距离支持面是多少d
例如时,代表样本在判别面正侧2d的位置,时则代表在负侧2d的位置
SVM的损失函数
由于SVM的支持面与判别面的距离为,所以两个支持面的距离为
最大化两支持面之间的距离,等价于最小化(给加平方是为了去掉根号)
硬间隔SVM的损失函数
硬间隔SVM最大化支持面之间的距离,并要求所有样本在支持面之外
因此,硬间隔的损失函数如下:
目标函数:
约束条件:,
✍️硬间隔约束条件解说:
正样本要在正支持面一侧,即,此时,可得
负样本要在负支持面一侧,即,此时,可得
软间隔SVM的损失函数
软间隔SVM最大化支持面之间的距离,并最小化错误样本
因此,软间隔的损失函数如下:
目标函数:
约束条件: (1) ,
(2)
其中,是对i个样本的松弛量,而C则是惩罚因子
✍️软间隔约束条件解说:
随着支持面的不同取值,有的样本能在支持面正确一侧,而有的则在错误一侧
不妨记为第i个样本的误错量,则第i个样本满足
然后目标函数则是最小化所有样本的总错误量,其中C是错误量在损失函数中的权重
备注:软间隔实际是硬间隔的扩展,因为当C极大的时候,软间隔模型就相当于硬间隔模型了
本节讲解SVM是如何求解的,以及损失函数对偶问题的相关内容
SVM是如何求解的
由于SVM的损失函数中带有各种约束条件,难以用一般方法进行求解
因此SVM的求解相对较为曲折,它不直接对损失函数求解,而是采取如下方法:
👉1. 先将损失函数转换为拉格朗日形式
👉2. 通过拉格朗日形式获得损失函数的对偶问题
👉3. 使用SOM算法求得对偶问题的解
👉4. 将对偶问题的解转换回原问题的解
SVM的损失函数与其对偶问题
由于SVM中一般只用软间隔模型,下面我们默认只讲述软间隔模型的求解
SVM损失函数-拉格朗日函数形式(软间隔):
将SVM软间隔模型的损失函数化为拉格朗日函数形式如下:
其中
SVM损失函数的对偶问题(软间隔)
软间隔损失函数的对偶问题如下:
目标函数:
约束条件: (1)
(2) ,
SVM对偶问题的解与原模型系数关系(软间隔)
在解得损失函数对偶问题的解之后,按下式可以转换回原问题的解
备注:以上几条公式看起来比较迷糊,初学者只需知道:
是先解得对偶问题的再用最后一条公式转换回w,b即可
SVM的模型表达式-支持向量形式
SVM的模型表达式-支持向量形式
由于SVM最终模型的解是由对偶问题的解所给出,因此SVM的表达式也可以写为以下形式:
其中
备注:中的指的是第i个样本的
忽略掉的项,可以看到,模型实际是由所有样本来共同表示
即的样本构成了最终的判别函数,因此,我们称的样本为支持向量
支持向量的几何意义
事实上,可以证明,支持向量是落在支持面上及支持面错误一侧的样本,如下:
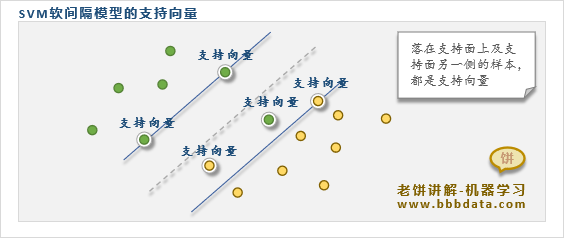
由此可知,支持向量是我们所需关注的样本,它们都是模型决策较为模糊、或错误的样本
由于模型的w,b实际只由支持向量构成,这就是为什么把模型称为"支持向量机SVM"的原因
本节通过实例来加深SVM的理解,以及展示如何使用SVM进行类别预测
SVM模型示例
下面通过一个例子展示SVM实现二分类的效果,以加深入SVM的理解:
from sklearn import svm
import numpy as np
# ----生成样本数据与构建SVM模型-----------
X = np.array( [[0.708333,1],[0.291667,1],[0.217,1.5],[0.2367,0.3],[0.454,1]
,[0.583333,-4],[0.875,-1],[0.333,-0.6],[0.111,-1]] )
y = np.array([1,1,1,1,1,-1,-1,-1,-1])
clf = svm.SVC(kernel ='linear',C=1000) # 初始SVM模型,这里C设为很大,也就成为了硬间隔
clf.fit(X,y) # 用X,y训练模型
# -----------------打印模型系数------------
print('\n---------支持向量与alpha--------') # 打印模型求解结果
print('support_vectors:\n',clf.support_vectors_) # 打印支持向量
print('alpha:\n' ,clf.dual_coef_[0]) # 打印支持向量系数
print("\n----------模型系数---------")
w = clf.coef_ # 提取模型系数w,它等于clf.dual_coef_[0]@clf.support_vectors_
b = -clf._intercept_ # 提取模型系数b
print('w:',w) # 打印模型系数w
print('b:',b) # 打印模型阈值b
# ---画出分割面与支持面-----------------
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (9, 5) # 设置figure_size尺寸
plt.scatter(X[:, 0], X[:, 1],c=y,marker='o') # 画出样本点
line_x = np.array([X[:,0].min(),X[:,0].max()]) # 判别面的x坐标
line_y = (-b-w[0,0]*line_x)/w[0,1] # 判别面的y坐标
plt.plot(line_x,line_y) # 画出判别面
line_u = (-b+1-w[0,0]*line_x)/w[0,1] # 上支持面的y坐标
line_b = (-b-1-w[0,0]*line_x)/w[0,1] # 下支持面的y坐标
plt.plot(line_x,line_u,color='grey') # 画出上支持面
plt.plot(line_x,line_b,color='grey') # 画出下支持面运行结果如下:
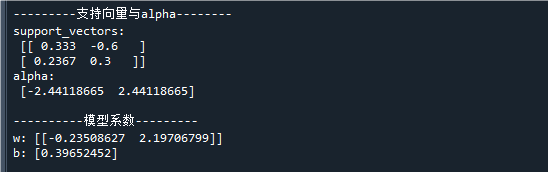
在代码中,我们将松驰惩罚系数C设得非常大(C=1000),相当于使用了硬间隔模型
在图中可以看到,SVM的支持面已经达到了样本的边界,即间隔最大化
其中正、负支持面各有一个支持向量,它们为与
最终得到的模型判别函数为:
SVM模型使用示例代码
下面展示如何使用SVM对乳腺癌问题进行类别识别的具体例子
乳腺癌问题的具体数据如下:
特征:平均平滑度、平均紧凑度、平均凹面、平均凹点,类别:0-恶性、1-良性
即以sk-learn中的breast_cancer的数据,breast_cancer原数据中有30个特征,为方便讲解,我们这里只选4个
用SVM实现乳腺癌类别识别的具体代码实现如下:
from sklearn import svm
from sklearn.datasets import load_breast_cancer
# ---加载数据-----------
data = load_breast_cancer() # 加载breast_cancer数据
X = data.data[:,4:8] # 作为学习,这里只选择breast_cancer数据中的4个变量进行建模
y = data.target # breast_cancer的y
#-----训练SVM模型--------------------
clf = svm.SVC(kernel ='linear',C = 4,probability=True) # 初始SVM模型
clf.fit(X,y) # 用X,y训练模型
#---------------模型预测结果------------------------
test_x = X[[0,101,201,301,401,501], :] # 测试数据的x
test_y = y[[0,101,201,301,401,501]] # 测试数据的y
y_pred_prob = clf.predict_proba(test_x) # 预测类别概率
y_pred = clf.predict(test_x) # 预测类别
#---------------打印结果---------------------------
print( "\n模型准确率:",sum(clf.predict(X)==y)/len(y)) # 打印模型的准确率
print("\n===打印模型系数:=====") # 打印模型参数
print('w:',clf.coef_ ) # 打印模型权重w
print('b:',-clf._intercept_) # 打印模型阈值b
print("\n===测试数据的真实类别:=====") # 打印测试效果
print(test_y) # 测试数据的真实y
print("\n===测试数据的预测概率:=====") # 打印
print(y_pred_prob) # 测试数据的类别概率预测结果
print("\n===测试数据的预测类别:======") # 打印
print(y_pred) # 测试数据的类别预测结果运行结果如下:
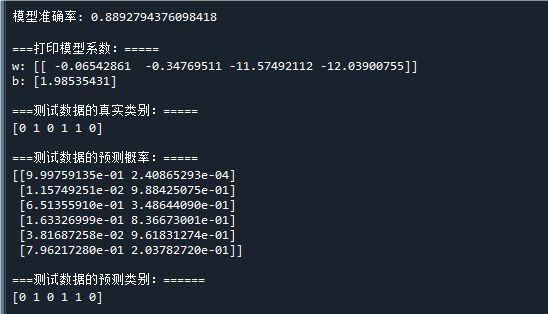
从预测结果可以看到,模型准确率到到88.9%,已经较好地预测了样本的类别
将 代回判别平面的表达式,可得到模型的判别函数为:
备注:SVM中,必须将模型设为probability=True,才可以预测概率
以上就是SVM支持向量机的全部入门内容了~
End
 评论
评论