
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
逻辑回归也称为logistic回归、逻辑斯蒂回归模型,它是机器学习中经典分类模型之一
本文讲解二元逻辑回归模型算法原理,包括逻辑回归的思想、模型、损失函数和求解方法等等
通过本文可以了解逻辑回归模型是什么,有什么用,以及逻辑回归的关键公式
在讲解逻辑回归算法原理前,本节先介绍什么是二分类问题
什么是二分类问题
逻辑回归模型主要用于二分类,即预测样本是正样本还是负样本
什么是二分类问题
现在有一组数据,需要利用各个特征去预测目标的类别是1还是0
数据如下:
这就是二分类问题,它的目的是判断类别样本属于哪个类别
二分类问题一般默认类别标签为0和1,只需判断是不是1类就可以了,因为不是1类则是0类
二分类问题的输出
二分类问题共有4种常见输出方式,如下:
1. 判断标签:直接输类别标签
2. 判断结果:输出Yes或No,即代表是不是类别1
3. 判断依据:输出属于类别0、1的判别值,哪类的判别值大就是哪类
4. 判断依据:输出属于类别1的概率
具体哪种输出更适合二分类问题,需要具体问题具体确定
但二分类问题输出概率是最通用的,因为它可以转化为判断标签或判断结果
本节讲解逻辑回归的原理与思想,以及逻辑回归模型的数学表达式
逻辑回归的模型原理与思想
数值与概率的正相关性
我们知道,线性回归拟合的是数值,并不符合二分类问题预测类别的需求
但数值与类别也是有关联的,即值越大,属于某类别的概率也越大
例如,天色越黑,下雨的概率就越大,因此判别值与概率之间可以相互转换
在数学里通常用函数 将数值转化为概率
sigmoid函数的图像如下:
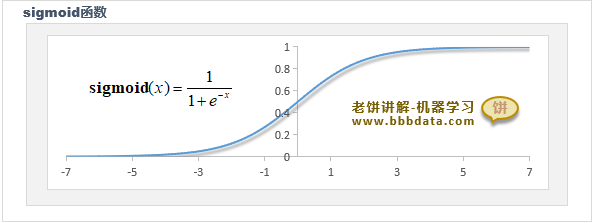
可以看到,sigmoid函数的输出区间为(0,1),它与概率的范围是一致的
逻辑回归模型的思想
逻辑回归就是这样的原理,先用 作为对样本类别的综合评估值,
再套用 sigmoid 函数将综合评估值转为概率所以,逻辑回归本骨子里还是线性模型
备注:这样理解逻辑回归模型的原理是不严谨的,但作为入门无伤大雅,
后面接触了信息熵的概念,再回头补充sigmoid函数的由来与实际意义
逻辑回归模型表达式
逻辑回归公式(模型表达式)如下:
备注:这里的X代表,最后的1用于替代b
逻辑回归模型特性解说
下面通过对逻辑回归模型的特性进一步了解逻辑回归原理
在单变量时,逻辑回归模型就是一条S曲线
类似地,在两个变量时,它就是一个S面,在更多变量时,则是一个超S面
其中,w控制了S曲线的拉伸,b则控制了它的平移位置,示图如下:
本节解说逻辑回归模型的损失函数及损失函数的设计思路
逻辑回归-损失函数-原理
损失函数引导我们去求取模型里的参数w和b,即指明我们想要求一个什么样的w,b
由于逻辑回归输出的是概率,采用均方误差作为损失函数就不适合了,它采用的是正确概率最大化~!
逻辑回归-单个样本评估正确的概率
对于单个样本,逻辑回归模型预测准确的概率为:
解释:逻辑回归的输出p就是样本属于类别1的概率
当真实标签y为1时, P就是评估正确的概率
真实标签y为0时,P是错误的概率,1-P 就是模型正确的概率
----------------------------------------------------
巧妙的操作是,可以用一条式子把上述二式合并如下:
当y=1时,第二个括号等于1;当y=0时,第一个括号等于0,故与上述两式一致
逻辑回归-所有样本评估正确的概率
假设每个样本是独立事件,
则逻辑回归总评估正确的概率为所有样本评估正确的积,如下:
逻辑回归的损失函数
我们期待 最大化,只要将损失函数设计成 即可
又由于 中含 有大量的乘号,为计算方便,我们外套一个对数
最后,损失函数设计如下:
在连乘的情况下,使用对数使其转为加号是常用的操作
因为对数是单调函数,能让P最大化的W,同样会是令lnP最大化的W
逻辑回归-损失函数
逻辑回归的损失函数如下:
其中,
逻辑回归损失函数设计的整体思路为:

这种思路设计的损失函数也叫最大似然损失函数
本节讲解逻辑回归模型损失函数的求解方法
梯度下降算法
现在我们需要训练逻辑回归模型,即求解逻辑回归模型里的参数W
使得损失函数 最小,也就是令预测概率准确性最大化
求解的算法比较多,但最经典的求解方法就是使用梯度下降算法
梯度下降算法原理如下:
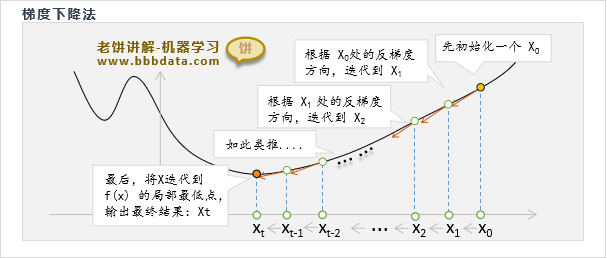
梯度下降算法先初始化一个解,然后不断地根据目标函数的负梯度方向调整x,直到达到局部最优值
具体理论请看《梯度下降算法原理》
逻辑回归-模型训练
逻辑回归模型训练流程
梯度下降训练逻辑回归模型的算法流程如下:
先初始化W,然后
1. 按照梯度公式算出梯度
2. 将W往负梯度方向调整
不断循环(1)和(2),直到达到终止条件(例如达到最大迭代次数)
逻辑回归-梯度公式
梯度下降法在迭代过程需要使用损失函数L(W)的梯度,
我们求出逻辑回归损失函数L(W)的梯度公式如下:
其中
X :矩阵, m样本数, n为特征个数
即一行为一个样本,一列为一特征
y : 样本的真实标签,列向量
p :模型预测的概率,列向量
公式的具体推导过程见《逻辑回归梯度公式推导》
笔者语:关于软件包里逻辑回归的训练算法
工具包里通常不使用梯度下降算法,对于训练逻辑回归模型,会有更巧妙的求解算法,
例如matlab工具箱里使用的就是牛顿法,它与梯度下降法思想类似
在这里我们先学习梯度下降法求解逻辑回归,作为入门理解,逻辑回归就已经足够了
梯度下降法是最经典必学的求解算法,没有之一,它简单,普适性广,通用
至于工具箱中逻辑回归所使用的算法,在进阶阶段再进行学习
好了,以上就是逻辑回归原理的全部内容了~
End