
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
在上张文章,我们借用sklearn包实现的,那软件内部是如何构造决策树的呢?
本文讲解决策树构建的具体详细过程,从而更具体、更细节的了解决策树是如何构建出来的
本文讲述的决策树构造原理来源于matlab源码,与sklearn的大同小异,但相对更为简洁
本节先梳理CART决策树究竟希望构建一棵什么样的树
CART决策树的构建目标
CART决策树的构建目标是构建一棵二叉树,尽量把历史样本按类别分到不同的叶子节点
最理想时,所有叶子的类别都只有一个,最不理想时,所有叶子的类别都平均
如下:
如图所示,CART决策树的构建目标就是令每个叶子节点的类别尽量清晰
本节讲解CART决策树的构建主流程,个别细节放在下一下节细讲
Step-1:根节点分裂
在决策树构建刚开始时,所有样本都在根节点,
此时先寻找一个特征和阈值,把样本一分为二,将样本分到左右节点
那怎么确定分裂时使用哪组【特征,分裂值】呢?
其实是靠历遍,历遍所有的【特征,分裂值】,然后评估收益,
哪组【特征,分裂值】分裂后的收益最大,就用哪组【特征,分裂值】
✍️说明:这里遗留两个CART决策树构建的细节放在下处讲解
👉 收益的具体评估方法
👉【特征,分裂值】的历遍
Step-2:判断新生节点是否继续分裂
当CART决策树分裂完根节点后,就产生了两个新节点
接下来需要判断,新生节点是成为叶子还是需要继续分裂
1.继续分裂
如果决策树的节点需要继续分裂,就继续寻找一个【特征,分裂值】,将节点继续一分为二
这就称为决策树的生长,示图如下:
2.成为叶子
如果成为叶子,将节点标为叶子,不再分裂,并将节点上样本最多的类别作为叶子类别
如果需要输出类别概率,就把该类别的占比一起记录下来
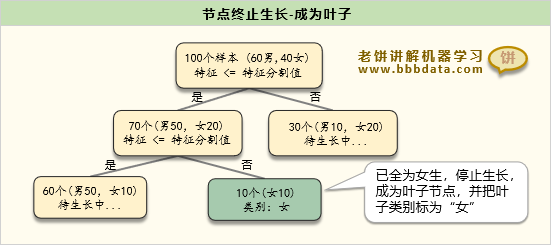
节点成为叶子的判别一般有以下几种条件:
(1)节点上的样本都属于同一个类别
(2)节点上的样本太少(例如,少于10个)
(3)节点层数过深(例如,节点层数>=10)
PASS:此类条件还有很多,不同软件包提供不同的条件选择
Step-3: 不断迭代直到终止
不断按Step-2去迭代,直到决策树中没有节点需要分裂
如图所示,当决策树中所有节点都成为叶子节点时,就停止生长
决策树构建-总过程
总的来说,决策树构建的过程如下:

1. 将所有样本作为根节点
2. 找到最佳的【特征,切割点】将根节点一分为二
3. 判断新节点是否成为叶子
如果新节点达到叶子条件就终止该节点的分裂,
如果未达到叶子条件,就继续分裂
4.如些反复,让节点分裂,直到最后所有末节点都是叶子节点
本节讲解上述主流程中,遗留的收益评估方法与【特征,分裂值】的历遍两个细节
节点分裂质量评估-收益函数GINI
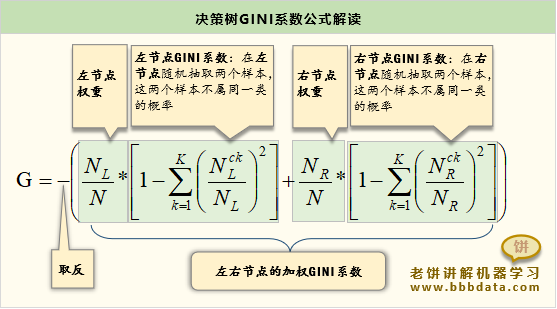
Gini收益函数公式
CART决策树一般用Gini基尼函数的取反函数作为收益函数来评估节点分裂质量
Gini函数如下:
其中
: 划到左节点的样本个数
: 划到右节点的样本个数
: 本次划分的总样本个数,即
: 左节点上属于 类的个数
: 右节点上属于 类的个数
GINI收益函数的含义
GINI收益函数整个公式的意思是,
在左(或右)节点随机抽取两个样本,这两个样本不属于同一类的概率
公式可以如下解读:
GINI系数为什么代表概率,请看《决策树GINI系数的推导》
✍️ GINI系数为什么能作为收益函数
同一个节点,不属同一类的概率越小(即属于同一类的概率越大),
说明节点上的杂质越小(也叫纯度越纯)
当一个节点的纯度达到最高,即节点上所有样本所属类别都一样时,
说明该节点说明分割得越好,这正是我们决策树构建中想要的结果
PASS:也可以用ID3中的熵作为收益函数,但CART中更主流的是使用GINI
【特征,分裂值】的历遍过程
决策树构建过程中,对【特征,分裂值】的历遍过程如下:
先对所有特征历遍,并找出每个特征的所有分割可能,
分别评估所有分割可能的收益,最后选择收益最大者,作为节点的【特征-分割值】
具体细节如下:
以上,就是matlab自带的fitctree函数构建一棵CART分类决策树的内部流程了
End