
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
为了进一步具体掌握梯度下降法,本文展示一个梯度下降算法求解二元函数最小值的例子
本文先用手算展示每一步的过程和结果,再展示python实现梯度下降算法的代码
通过本文,可以具体地了解梯度下降算法是如何求解最小值的,以及它的代码实现
本节梳理梯度下降法在实际使用时的流程
梯度下降算法-实现过程思路梳理
梯度下降算法简单来说,就是将解按负梯度方向不断迭代,直到满足终止条件
由于需要用到目标函数梯度,所以一般需要先算出梯度公式,以方便迭代过程中计算梯度
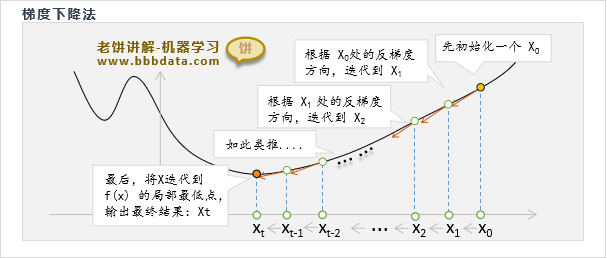
总的来说,梯度下降算法在实现过程中,需要如下四步:
1. 梯度公式准备 :计算目标函数的梯度
2. 初始化解与参数 :设置好解的初始值和学习率
3. 按负梯度更新解 :按照负梯度将解不断迭代
4. 终止条件判断 :直到梯度极小,就停止迭代
本节通过手动计算,展示梯度下降算法的每一步具体操作
梯度下降实例-问题
求二元函数的最小值
求 为何值时,取得最小值
其中:
易知道,
在 处取得的最小值为0
下面展示用梯度下降法寻找解的具体过程,看结果是否与我们预期一致
梯度下降算法-手算具体过程
使用梯度算法求解上节的问题是较为简单的,
作为学习例子,我们展示整个手算过程如下
1、梯度公式计算
由 ,
有
2、参数设定
现设初始值为,
此时
3、迭代
迭代1:
计算梯度 :
更新x :
查看 y值 :
迭代2:
计算梯度 :
更新x :
查看 y值 :
...............
...............
...............
迭代40:
计算梯度 :
更新x :
查看 y值 :
4、结果
第40次迭代时,与都极小,我们退出迭代 ,
以 作为最终结果,此时函数值
易知,与预期的 x= [2,3] , y=0 几乎一致。
本节利用python进行代码编程,展现如何用代码实现梯度下降算法
梯度下降算法-代码实现
"""
本代码用于展示,梯度下降求y= (x1-2)^2+(x2-3)^2的最小解
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
x1 = 0 # 初始化x1
x2 = 0 # 初始化x2
for i in range(100): # 迭代100次
#------计算梯度--------
dx1 = 2*x1-4 # 计算x1的梯度
dx2 = 2*x2-6 # 计算x2的梯度
#----- 往负梯度方向更新x------
x1 = x1 - 0.1*dx1 # 将x1往负梯度方向更新
x2 = x2 - 0.1*dx2 # 将x2往负梯度方向更新
#----- 判断终止条件 --------
if((abs(dx1)< 0.001) & (abs(dx2)< 0.001)): # 如果梯度过小
break # 则退出迭代
print("第",i+1,"轮迭代:x=[",x1,",",x2,"],y=",(x1-2)**2+(x2-3)**2) # 打印结果 代码运行结果如下:
以上就是梯度下降算法实例与代码的全部内容了~
End