本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
梯度下降法是一种基本的函数优化算法,在机器学习中经常使用它来训练模型
本文分析和讲解梯度下降算法的优点和缺点,以及这些优点和缺点所带来的影响
通过本文,可以了解梯度下降算法有哪些优点和缺点,同时加深对梯度下降算法的理解
本节探讨梯度下降算法的几个优点
梯度下降算法的优点
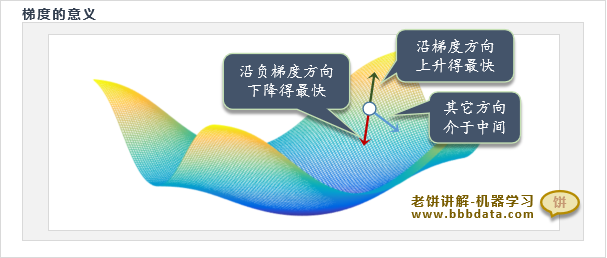
梯度下降法以负梯度方向来迭代x,使目标函数能最速下降,因此也称为最速下降法
梯度下降法的优点如下:
1.必能下降
按负梯度调整,加上学习率的控制,则能保证x的调整,函数一定能下降
2.下降速度快
按负梯度下降,由于负梯度是下降最快的方向,在下降速度上更加有效
所谓最快,即调整同样的步长,该方向能令函数下降最快
3.算法简单有效
梯度下降法只需求一阶导,且迭代机制也简单,相对其它算法更为简单
因此不管是推导、计算、代码编写上都非常简单明了,且效果不错,性价比非常高
✍️笔者语
笔者刚入门时,觉得梯度下降法真厉害,因为它能使目标函数最速下降!
然而,好些年后才发现,梯度下降最卓越的地方不在于它下降最快,而是它能保证下降!
正是因为梯度下降法能保证下降,因此有许多算法,可以采取"更大胆的算法策略“来下降
当"大胆策略"能下降时,就用"大胆策略",当"大胆策略"不能下降时,则退化为梯度下降
如此一来,进可攻退可守,既可以放心大胆地去下降,又有梯度下降算法进行兜底
也正是因此,梯度下降作为一种经典算法,在其它算法中仍然能经常看到它的身影~
本节探讨梯度下降算法的几个缺点
梯度下降算法的缺点
梯度下降算法的缺点如下:
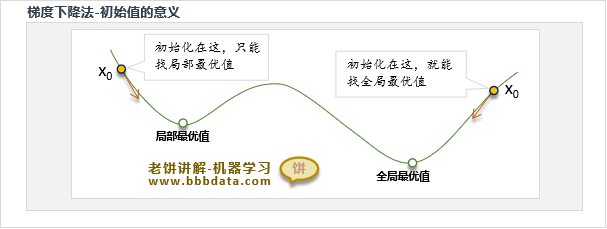
缺点1.只能找到离初始值最近的局部最优
梯度下降算法遇到局部最优时,算法就停止,因为此时梯度为0
因此,梯度下降法只能找到离初始解最近的局部最优,对跳出局部完全无反抗能力
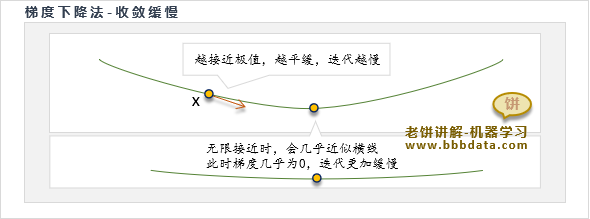
缺点2.收敛速度慢
梯度下降法在梯度平缓处的迭代速度较慢,而极值附近一般都是相对较为平缓的,
因此,当无穷接近极值处时,梯度下降算法的迭代会变得无穷慢,即收敛速度缓慢
好了,以上就是梯度下降算法的优缺点了~
End
 评论
评论