本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
线性回归模型一般作为机器学习入门的首选模型,它包括了模型的核心内容
本文对线性回归模型进行简单总结,是对线性回归模型知识点的简化与提炼
通过本文,进一步沉淀线性回归的相关内容,同时加深对机器学习模型的理解
本节总结线性回归的模型表达式、损失函数和模型求解方法
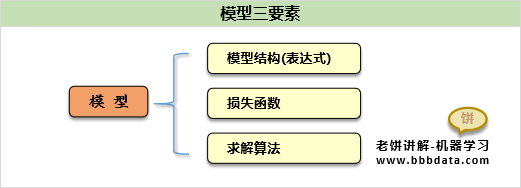
线性回归-模型三组件
模型的三组件为:《模型》《损失函数》《模型求解》
线性回归模型的三组件如下:
线性回归的模型表达式
线性回归的损失函数
线性回归的损失函数用的是最小均方差
线性回归的模型求解
线性回归的模型的求解直接使用最小二乘法求解就可以
✍️备注:这里的X对原始变量增加了一列常数1,即
W也对应地比原来多一个,这样做的目的是把 b揉进了W里
本节回顾利用线性回归进行建模的过程
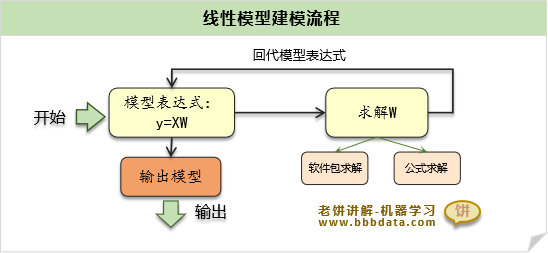
线性回归-建模过程回顾
线性回归建模过程如下:
(1) 先假设变量与y服从线性关系 y= XW
(2) 按公式对W进行求解
(3) 将求解的W代入模型
✍️补充
在使用线性回归模型时,需要判断x与y是否成线性关系,
这依赖于我们对业务背景的了解,和变量的数据分析
好了,以上就是线性回归总结的所有内容了~
End
 评论
评论