
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
PCA主成份分析常用于降维与变量分析,是一个基本、知名度极高和常用的方法
本文介绍PCA的原理和本质,以及相关使用场景的用法,并通过实例讲解如何使用PCA
通过本文可以快速了解PCA是什么,如何使用PCA进行变量分析以及使用PCA对变量降维
本节介绍PCA用于解决什么问题及PCA的思想,初步了解PCA是什么
主成份分析思想
主成份分析PCA(Principle Component Analysis)的主要功能是去除变量之间相关性
去除相关性也可理解为去除信息冗余,因此PCA常用于降维和排名等问题
什么是变量间的信息冗余
如上所示,可以明显看到x1和x2是相关的,它们之间存在着线性信息冗余
例如知道x1很大,那就知道x2也小不到哪去,所以x1和x2之间存在信息冗余
主成份分析解决变量相关的思路
主成份分析PCA是如何解决变量相关的问题的呢?很简单,如下所示:
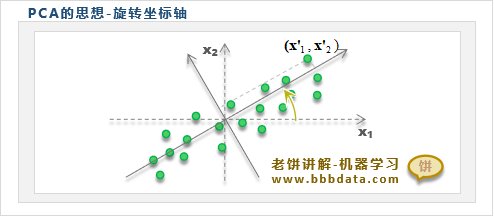
PCA的思路就是将坐标轴旋转,让样本在旋转后的坐标中各个维度都不相关
✍️通过旋转样本来理解PCA
也可以用如下的思路理解PCA:将样本旋转,使旋转后的样本在各维不相关

总的来说,PCA的核心思想就是将样本或坐标轴进行旋转,使得各维之间互不相关
PCA的数学表述
PCA的模型表示
PCA就是对样本进行旋转,而旋转变换在数学中就是一个标准正交矩阵A
因此,PCA的模型表达式为:
其中,A为标准正交矩阵
✍️解释:它代表先将数据进行中心化,然后再进行旋转
PCA的求解目标
由于PCA要求旋转后的样本每个维度互不相关,即Y的协方差矩阵为对角矩阵
因此,PCA的求解目标函数为
其中, 为对角矩阵
本节介绍在PCA中,主成份以及主成份方差的意义
PCA中的方差与主成份贡献
样本经过PCA旋转后,样本各维之间没有信息冗余,即它们之间的信息是独立的
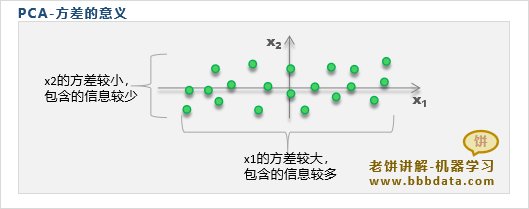
因此,PCA用各维的方差来代表该维所贡献的样本信息大小,用方差占比作为贡献
例如,y1、y2 的方差为8和2,则认为y1贡献了80%的样本信息,y2贡献了20%的信息
通过方差占比,可以知道哪些维是重要的、哪些维不重要,可以依此来进行相关分析
更常用的是,直接忽略一些不重要的维(即方差占比较小的维),从而起到降维的作用
✍️补充为什么维度的方差可以代表该维包含的样本信息量?
因为信息来自于不确定性,当某维方差越大,样本在该维就越不确定,信息也就越多
极端地,如果某维的方差为0,即所有样本在该维是一样的,此时也就没任何信息可言
PCA的主成份与主成份系数
主成份与主成份系数
在PCA中,把旋转后得到的各个变量称为主成份
并根据方差从大到小,命名为第一主成份(方差最大)、第二主成份(方差第二大).....
而第个主成份的系数(即中的),则称为主成份的主成份系数
PCA中对主成份的约定
在PCA中默认约定,在A中的第 列分别存放第 主成份的系数
如此一来,实际就是第主成份,它们的方差由大到小
本节讲解PCA的一般使用场景,进一步具体了解PCA有什么用
PCA主成份的应用
使用PCA时,一般需要计算出主成份系数以及打印主成份贡献占比
PCA的具体使用过程如下:
1. 计算主成份系数A
用X求出主成份系数A
2. 计算主成份y
通过计算主成份
3. 计算贡献占比与累计占比
贡献占比就是主成份y的方差占比
PCA主成份变量分析
变量之间往往存在信息冗余,在对变量分析时,先进行PCA可以更清晰地分析变量
如上图所示,可以看到,X中70%的信息由表示,而剩下信息基本由表示
因此,X虽然有5个变量,但实际信息只有3个变量,说明 X中存在较多的信息冗余
PCA降维
PCA降维是指只用其中一部分主成份来替代原始变量X,从而达到变量降维的效果
由于每个主成份的主成份贡献(方差占比)就代表了该主成份所包含的样本信息占比
因此,可以忽略一些主成份贡献占比较小(信息少)的主成份,从而起到降维的作用
如上图所示,可以看到,只需要取前3个主成份时,主成份总贡献就已经达到了95%
因此,可以忽略掉其它次要的主成份,只取前3个主成份来代表原来的样本数据即可
变量过多易引起模型过拟合,通过PCA降维后再进行建模,模型效果往往会得到改善
✍️老饼语: PCA的特点主要为:(1)去除变量的信息冗余,(2)减少变量个数
只要有以上两个需要,都可以考虑使用PCA来尝试解决
本节通过一个实例展示如何实现与使用PCA主成份分析
PCA代码与例子
下面先通过sklearn包来实现一个PCA例子,对iris数据进行降维
# -*- coding: utf-8 -*-
"""
主成份分析使用DEMO
本代码来自老饼讲解-机器学习:www.bbbdata.com
"""
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import numpy as np
# 加载数据
iris = load_iris() # 加载iris数据
X = iris.data # 样本X
x_mean = X.mean(axis=0) # 样本的中心
# 用PCA对X进行主成份分析
clf = PCA() # 初始化PCA对象
clf.fit(X) # 对X进行主成份分析
# 打印结果
print('\n主成份系数矩阵A:\n A=',clf.components_) # 打印主成份系数
print('主成份方差var:',clf.explained_variance_) # 打印主成份方差
print('主成份贡献(方差占比)Pr:',clf.explained_variance_ratio_) # 打印主成份占比
print('主成份累计贡献(方差累计占比)Pr:',np.cumsum(clf.explained_variance_ratio_)) # 打印主成份累计占比
# 获取主成份数据
y = clf.transform(X) # 通过调用transform方法获取主成份数据
y2= (X-x_mean)@clf.components_.T # 通过调用公式计算主成份数据 运行结果如下:
可以看到,经过PCA转换后,第一主成份贡献达到92.4%,第二主成份贡献占比为5.3%
这说明iris数据的4个变量存在严重信息冗余,它们的信息大部分可由第1、2主成份表示
如果需要对其进行降维,可以只取前两个主成份,它们的累计贡献已达到97.7%
好了,以上就是PCA主成份分析的使用例子和原理解说了~
End