本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
牛顿法是一种应用于函数优化问题(即求极值)的算法,它源自于牛顿求根法
本文介绍牛顿法的迭代公式、算法流程以及详细的推导过程,并展示牛顿求极值的具体例子
通过本文可以快速理解牛顿法的算法流程、迭代公式和原理推导,以及牛顿法的具体代码实现
本节简单介绍牛顿求极值是什么及本文的讲解思路
什么是牛顿法
牛顿法是一种基于牛顿求根法而衍生出来的函数优化算法
设是一个多维向量,求 的极值
牛顿法的算法流程如下:
1. 设置一个初始解
2. 按以下公式迭代,直到满足终止条件
其中:
G为梯度(Gradient)(F的一阶偏导)
H为Hession矩阵(F的二阶偏导矩阵 )
由于牛顿法利用了二阶导信息,它的迭代速度比梯度下降法要更加快,
但同时,由于二阶导信息的计算量较为复杂,牛顿法的使用往往没有梯度法广泛
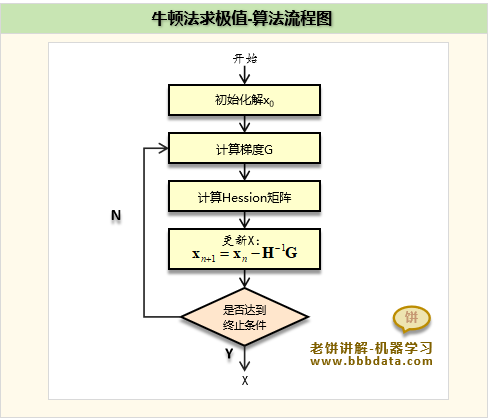
牛顿法求极值算法流程图
牛顿法求极值的算法流程图如下:
本节讲解牛顿法的原理,以及牛顿法迭代公式的推导
牛顿求根法
牛顿求极值方法的思想来源于牛顿求根法,它是牛顿求极值的前身
下面先讲解牛顿求根法,更为方便后面理解牛顿求极值法的思路
函数求根,即求函数 时的取值
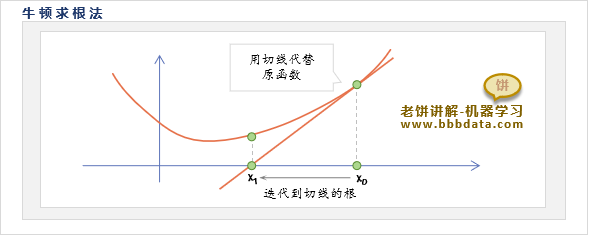
牛顿求根法是解决函数求根的一种迭代方法,它的思路如下:
由于函数在任一个点附近都可用其切线近似替代
某种程度上,可用该点的近似函数(切线)的根 来近似原函数的根
但由于仅仅是近似,不够准确,因此牛顿求根法通过反复迭代来不断逼近原函数的根
即从开始,然后用公式: 不断地迭代,直到已极度近似0
牛顿求根法具体算法流程如下:
1. 设置一个初始解
2. 按公式 进行迭代,直到满足退出条件
退出条件:已极度近似0,或者达到最大迭代次数
牛顿法求极值
下面先讲牛顿法对一维函数求极值的思路,再进一步拓展到多维
牛顿法一维函数求极值
一维函数求极值,即求一维函数取得极值时 x 的取值
现在我们要求取 的极值,可借用牛顿求根法思路如下:
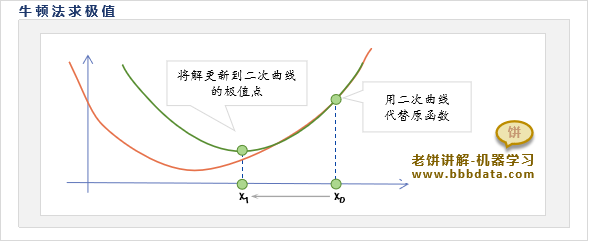
1. 设初始点为
2. 在该点附近函数可用该点的近似二次曲线替代:
根据泰勒展开,即可得到处的二次近似曲线为:
3. 用该近似函数( 二次曲线) 的极值作为新的解
推导过程如下:
的极值点在一阶导等于0处取得,则有:
,即
进一步即可得到
综上可得,牛顿法求一维函数的极值时,迭代公式为:
牛顿法求多维函数求极值
牛顿法多维函数求极值与一维的思路是类似的
1. 在 处的近似二次曲面为:
2. 该二次曲面的极值点即其一阶导等于0处:
即得:
一阶导称为梯度(Gradient),记为G ,二阶导称为Hession矩阵,记为H
则上式可简记为:
综上所述,即可得到牛顿法多维函数求极值的迭代公式:
其中,:梯度(一阶导)
:的Hession矩阵(二阶导)
本节讲解牛顿法求极值的代码实现例子
牛顿法求极值-代码实现
现使用牛顿法来求二元函数的最小值
由于牛顿法需要使用目标函数的梯度和Hession矩阵,现计算如下:
一阶导: ,
二阶导:
即:
根据G,H的公式,使用迭代公式 不断迭代即可
具体代码如下:
# -*- coding: utf-8 -*-
"""
牛顿法求y= (x1-2)^2+(x2-3)^2的最小解
"""
import numpy as np
x = np.array([0,0]) # 初始化x
for i in range(100): # 最大迭代100次
G = np.array([2*x[0]-4, 2*x[1]-6]) # 计算梯度G
H = np.array([[2,0],[0,2]]) # 计算Hession矩阵
x = x -np.linalg.inv(H)@G # 使用牛顿法迭代公式进行迭代
if((min(abs(G))< 0.001) ):break # 如果梯度过小,则退出迭代
print("\n第"+str(i+1)+"轮迭代:x=:["+str(x[0])+","+str(x[1])+"],y="+str((x[0]-2)**2+(x[1]-3)**2))运行结果如下:
可以看到,一步就迭代到了,这是因为目标函数本身就是二次函数的原因
牛顿法的好处就在于,它是二次收敛的,它最大的缺点是需要计算Hession矩阵及其逆
好了,关于牛顿法优化目标函数的内容就讲到这里了~
End