
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
感知机(perceptron)由Rosenblatt在1957提出,用于解决二分类问题,是BP与SVM的前身
本文讲解感知机模型的模型、损失函数,以及训练原理,并展示一个感知机实现代码例子
通过本文,可以快速了解什么是感知机模型,以及如何使用感知机模型对样本进行二分类
本节讲解感知机的模型数学表达式以及损失函数,初步认识感知机是什么,用于做什么
感知机的模型数学表达式
感知机(perceptron)模型是一个线性模型,它主要用于做二分类
在输入为二维的时候,感知机就相当于找出一条直线
将平面一分为二,一边为正样本,另一边为负样本
感知机模型的数学表达式为:
其中:
当y=1时为正样本,y=-1时则为负样本
感知机的损失函数
感知机的目标函数
感知机希望错误样本越少越好,即最小化以下误差E:
其中,,即感知机对第i个样本的预测值
考虑到上述目标函数不利于求导,因此模型训练时使用的是如下损失函数
感知机的损失函数
感知机的损失函数为:
✍️感知机损失函数意义解说
(1) 当网络对第i个样本预测正确时:
为正,为 1,则 为正
为负, 为-1,则 为正
(2) 当网络对第i个样本预测错误时:
为正,为 -1,则 为负
为负,为1,则 为负
综合则有:
预测正确时,为正
预测错误时,为负
因此,网络越正确,L(w,b)越小,网络越错误,L(w,b)越大
则我们要令L更小,只要往w和b的负梯度方向调整即可
本节讲解感知机是如何训练的,以及感知机的训练算法流程
感知机的训练算法流程
感知机一般用单样本训练,即逐个样本训练w、b
如果当前训练样本的预测值与真实值不一致,就往负梯度方向更新w,b
感知机第i个样本的损失函数对 w 和 b 的梯度如下:
感知机的具体训练流程如下:
1、初始化
将w和b的元素全部初始化为0
2、逐样本训练
逐个样本训练 w,b,
如果训练样本的预测值与真实值不一致
则往负梯度方向更新w,b( 其中,lr为学习率):
3、检测是否终止训练
如果达到训练终止条件,则终止训练,否则重复2
训练终止条件如下:
👉 (1) 总体预测误差达到目标
👉 (2) 达到最大训练步数
误差的评估公式如下
4、输出结果
训练完后,输出如下结果
👉w:感知机的权重
👉b:感知机的阈值
👉E:预测误差
✍️补充说明
已被证明,在样本点可分的情况下,算法经过有限次迭代,感知机肯定能将样本完全分开
证明可参考 李航-《统计学习方法》2.3.2节
本节展示感知机模型的实现例子与代码
感知机模型的实现代码
下面展示如何使用python的sklearn实现一个感知机模型
在sklearn中使用Perceptron实现在一个感知机,详细示例代码如下:
from sklearn.linear_model import Perceptron
import numpy as np
# ----生成样本数据-----------
X = np.array( [[0,0],[0,1],[0.2,0.5],[1,0],[1,1],[0.8,0.3]] )
y = np.array([1,1,1,-1,-1,-1])
# -----训练感知机模型--------
clf = Perceptron(eta0=0.1,max_iter=10000) # 初始化感知机模型,并设学习率为0.1
clf.fit(X,y) # 训练感知机
y_pred = clf.predict(X) # 对样本进行预测
acc = sum(y==y_pred )/len(y) # 统计准确率
w = clf.coef_ # 提取模型权重
b = clf.intercept_ # 提取模型阈值
# -----打印结果---------------------
print('\n模型准确率:',acc) # 打印准确率
print('模型权重w:',w) # 打印权重w
print('模型阈值b:',b) # 打印阈值b
# -----画出分割平面------------------
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1],c=y,marker='o') # 画出样本点
line_x = np.array([X[:,0].min(),X[:,0].max()]) # 判别面的x坐标
line_y = (-b-w[0,0]*line_x)/w[0,1] # 判别面的y坐标
plt.plot(line_x,line_y) # 画出判别面运行结果如下:
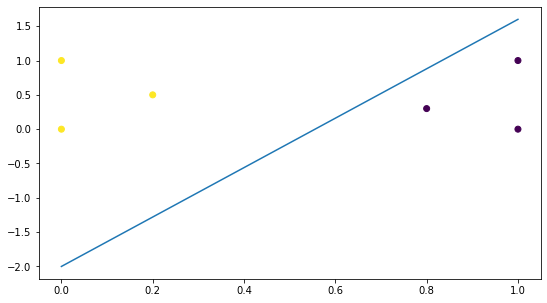
可以看到,模型已经正确地对样本进行划分,能准确地预测样本类别
好了,以上就是感知机二分类模型的原理与使用方法了~
End