
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
SVD降维是一种利用SVD分解来使矩阵降维的方法,属于一种有损降维
本文讲解SVD降维的具体流程,以及展示一个SVD降维的使用例子与实现代码
通过本文可以快速了解什么是SVD降维,如何使用SVD降维,以及了解降维的效果
本节简单讲述SVD分解,并通过讲解SVD降维的流程来快速了解什么是SVD降维
什么是SVD分解
SVD分解是指对矩阵A作如下分解 :
m*n矩阵A,将其分解为、 和 三个矩阵,如下
其中,
:m*m的酉矩阵
:m*n半正定对角矩阵
:n*n的酉矩阵
(1) 通常 对角元素由大到小排序,这样 、和是唯一的
(2) 对角线上的元素称为A的奇异值
SVD降维及操作流程
要了解什么是SVD降维,不必看太多文字描述,直接看一下它的流程就能自然明白
SVD降维操作流程
使用SVD进行降维的流程如下:
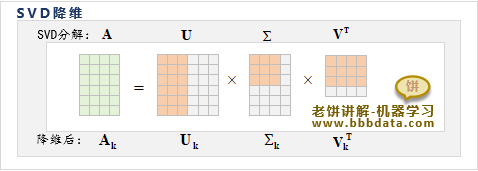
1. SVD分解
对目标矩阵进行SVD分解,得到 三个矩阵
即
2. 截取
忽略较小的奇异值,截取,从而获得近似矩阵
即如果的第k个奇异值较小,则截取,得到:
其中
:的前k列
:的前k行、前k列
:的前k行
3. 降维存储
用 替代进行存储
因为与近似, 而可以拆解成和进行记录
它们的记录量比直接记录A更加少,从而起到压缩的效果,这就是SVD降维
✍️为什么SVD降维后的存储量更加少
为什么存储和比直接存储A更加少?
不妨看下两者所需的存储量:
(1) 存储A需要存储数字个数:
(2) 存储需要存储数字个数:
由于大小为,大小为,大小为,则有:
所以当 较小时,后者的存储量就比前者要小
本节展示SVD降维的实际例子,加深对SVD降维的理解
SVD降维实例
下面以图片(即一个矩阵)为示例,展示SVD降维的应用及效果
如上,图片的像素为349*284,直接记录的存储量为349*284=99116
下面我们取不同的k值对它进行SVD降维,python代码实现如下:
import math
import numpy as np
from numpy.linalg import svd
import matplotlib.pyplot as plt
from PIL import Image
# 读取图片
x = Image.open("D:\\flower.png") # 读取图片
U,S,V = svd(x, full_matrices=False) # 对图片进行SVD分解
m,n = x.size # 图片的大小
fig, axes = plt.subplots(2, 3,figsize=(8, 6)) # 初始化画布
plt.subplots_adjust(wspace=0.2, hspace=0.3) # 调整子图之间的间隔
axes[0, 0].imshow(x,cmap="gray") # 绘制原图
axes[0, 0].set_title('k=full,(data='+str(m*n)+')') # 显示原图的大小
k_list = [100,50,25,10,5] # 设置k的大小
for i in range(len(k_list)): # 逐个k压缩图片
k = k_list[i] # 当前k
Uk = U[:,:k] # 截取U前k列
Sk = S[:k] # 截取S前k个元素
Vk = V[:k,:] # 截取V前k行
xk = Uk@np.diag(Sk)@Vk # 计算压缩后的x
data_num = m*k+k+n*k # 计算压缩后的数据量
idx = (math.floor((i+1)/axes.shape[1]),(i+1)%axes.shape[1]) # 当前图片索引
axes[idx].imshow(xk,cmap="gray") # 绘制图片
axes[idx].set_title('k='+str(k)+',(data='+str(data_num)+')') # 显示图片数据量
plt.show() # 显示画布运行结果如下:

可以看到,SVD降维的效果整体是不错的
当k=50时,它的存储量为31700,只有原图的1/3,但图片质量与原图没太大差异
随着k 的取值越小,SVD降维后的所需存储的数据量越小,同时信息损失也在扩大
但不管k 的取值如何,它总能在有效减少数据量的同时,保持住原图片的核心信息
End