本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
协方差常用于评估变量与变量间的相关性,它是基本的统计指标之一
本文介绍协方差的定义和计算公式和原理,并进一步介绍协方差矩阵与代码实现
通过本文,可以快速了解协方差、协方差矩阵是什么,以及如何使用协方差评估变量与变量的相关性
本节介绍协方差的意义及计算公式,并分析它的原理
协方差定义与公式
在统计学上用协方差来评估两个变量是否相关
协方差的定义及计算公式如下:
当协方差为0时,则说明两个变量不相关
协方差为什么能评估变量的相关性的
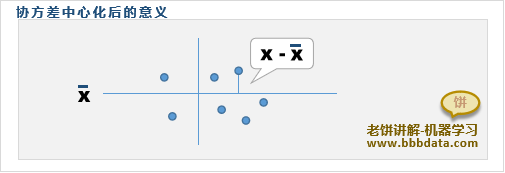
下面我们分析一下协方差为什么能评估变量的相关性的,加深对协方差的理解
记 , ,则与分别代表X和Y相对中心的偏移量
因此协方差是X与Y偏移量对应相乘再相加:
下面分别对X与Y相关、X与Y不相关两种情况进行分析与讨论
1. X与Y不相关
如果X与Y不相关,X的偏移方向与Y的偏移方向也就不相关
即Y'是正是负与X'是否是负无关,是正(或负)的概率为50%
则的期望就是0
2. X与Y相关
如果X与Y正相关,X的偏移方向与Y相同,即同号
因此的期望大于0
类似地,负相关时,X的偏移方向与Y相反,X'、Y'一正一负
则X'*Y'的期望小于0
本节介绍协方差矩阵是什么,并展示代码实现的DEMO
协方差矩阵是什么
什么是协方差矩阵
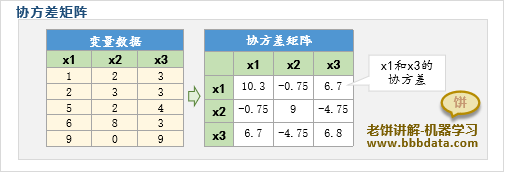
多个变量时,变量间两两之间的协方差系数,就组成了协方差矩阵
通过协方差矩阵,可以比较一目了然看到变量间的协方差
协方差矩阵如下图所示:
协方差矩阵的计算
设X为m行n列的数据,每列代表一个变量,
则X的协方差矩阵计算如下:
1. 先将X中心化:
2.再用中心化的X'计算协方差矩阵:
协方差矩阵计算-代码实现
下面展示如何使用python计算协方差矩阵,包括用公式计算及调用numpy函数计算
具体代码如下:
"""
求协方差矩阵的Demo
"""
import numpy as np
X = np.array([[1,2,3],[2,3,3],[5,2,4],[6,8,3],[9,0,9]]) # 原始数据
#----------使用公式计算协方差矩阵------------
Xn = (X - X.mean(axis = 0)) # 原始数据中心化
C = Xn.T@Xn/(X.shape[0]-1) # 计算协方差矩阵
# ---------使用numpy计算协方差矩阵----------
Cp = np.cov(X.T) # 计算协方差矩阵
print('\n数据X:\n',X) # 打印数据
print('\n使用公式计算的协方差矩阵C:\n',C) # 打印公式计算的协方差矩阵
print('\n使用numpy计算协方差Cp:\n',Cp) # 打印numpy计算的协方差矩阵运行结果如下:
可以看到,使用公式与使用numpy计算协方差矩阵是一样的
好了,协方差、协方差矩阵及协方差的意义就介绍到这里了
End