本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
岭回归模型的求解与线性回归类似,但由于岭回归中加入了惩罚项,所以略有不同
本文展示岭回归的求解公式,并给出求解公式的推导过程
本文展示如何自写代码实现岭回归模型的求解通过本文可以更具体的掌握岭回归模型的实现原理
本节展示岭回归模型的求解公式和推导过程
岭回归模型回顾
岭回归的模型表达式
岭回归模型表达式的矩阵形式如下:
岭回归的损失函数
岭回归损失函数的矩阵形式如下:
其中 是正则项的惩罚系数,代表参数W的惩罚力度
岭回归模型求解公式
岭回归模型求解公式
岭回归的模型求解公式如下:
它与线性回归的求解公式相似,只是部分需要在对角元素上加上
岭回归求解公式推导过程
只要令岭回归的损失函数L对W的各个偏导数为0,然后对其求解就可求得令L最小化的W
岭回归求解公式推导过程如下:
一、L(W) 对 W求导
二、令导为0 ,即可解得 W
本节介绍岭回归模型求解的算法流程与相关公式
岭回归的求解-算法流程
岭回归模型(带阈值)的求解流程如下:
主流程中各个步骤的相关公式如下:
1. 数据中心的计算
2. 数据中心化
3. 模型权重求解公式
4. 模型阈值求解公式
sklearn岭回归求解的核心源码
我们不妨看下sklearn中岭回归求解的核心实现代码:

从源码可以看到,W的求解就是计算公式
本节展示如何自写代码来实现岭回归模型
自写代码求解岭回归
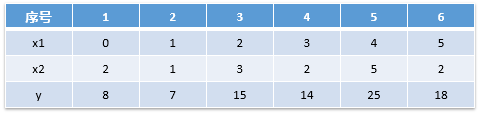
现有数据以下,需要我们建立岭模型,用变量 x1,x2 预测y
备注:以上数据的实际关系为:
下面实现一个带阈值的岭回归模型
根据《岭回归-算法流程》的求解流程, python代码如下:
# 本代码展示如何自实现岭回归
# 转载请说明来自 《老饼讲解机器学习》 www.bbbdata.com
import numpy as np
#--------------------输入数据----------------
x = np.array([[0, 2], [1, 1], [2,3],[3,2],[4,5],[5,2]]) # 输入数据x
y = np.array([8,7,15,14,25,18]) # 输出数据y
# 参数设置
alpha = 1 # 设置惩罚系数alpha
#--------------------模型求解----------------
# 计算数据的中心点
xm = x.mean(axis=0) # x的中心点
ym = y.mean(axis=0) # y的中心点
#将数据进行中心化,再用公式求解基础岭回归的权重
X = x - xm # 对x进行中心化
Y = y - ym # 对y进行中心化
w = np.linalg.inv(X.T@X+np.eye(x.shape[1])*alpha)@X.T@Y # 用公式求解权重
# 计算原始数据对应的模型阈值
b = ym-(w@xm) # 计算模型阈值
#输出模型系数和阈值
print("当前alpha:"+str(alpha))
print("模型参数:"+str(w))
print("模型阈值:"+str(b))运行结果如下
当前alpha:1
模型参数:[1.97256098 2.72865854]
模型阈值:2.7469512195121943
可以看到,它的实现效果与《sklearn实现岭回归》的结果是一致的
这侧面说明这与sklearn内部的实现基本是一样的
End